|
Любые вопросы по всем формам ГИА - ОГЭ и ЕГЭ
|
|
|
Александр_Игрицкий | Дата: Четверг, 07.01.2016, 14:03 | Сообщение # 361 |
| Сообщений: |
11095 |
| Награды: |
129 |
| Статус: |
Offline |
|
miflin, напомню, что все приводимые аргументы должны быть понятны школьнику и использовать известные законы и понятия.
Цитата miflin (  ) От неравномерного распределения плотности поверхностного заряда.
Согласен. Как это объяснить школьнику "на пальцах"?
Цитата miflin (  ) В результате электростатической индукции.
Я не против, если понять, как в результате на нейтральной пластине родился избыточный заряд. Индукции это не по зубам.
Цитата miflin (  ) 1. Можно в симметричной точке поместить заряд противоположного знака, а плоскость убрать, т.к. наведенный
на ней заряд исчезнет. Это называется "метод изображений".
Отличный способ, поскольку очень мощный и универсальный. Недоступность его реализации в полном объеме для школьников не делает его менее понятным. Но можно и по-другому. Напишу.
Цитата miflin (  ) 2. Если по каким-то соображениям введение фиктивного заряда претит , то можно использовать факт отсутствия
поля в другой части полупространства (см. картинку выше).
Моё отношение к этому примерно такое.
Смотрим на картинку, из которой видно, что поля в другой части нет. Что и требовалось доказать.
Цитата miflin (  ) Из решения уравнения Лапласа "методом изображений" для данного частного случая.
Нет, не соглашусь.
Меня может устроить только точное решение уравнения Лапласа для такой задачи.
Над центром плоского незаряженного проводника, имеющего форму шайбы с радиусом R и толщиной d, расположен на расстоянии h точечный заряд Q. Найти распределение поля во всем пространстве и распределение заряда по поверхности шайбы. Предельными переходами к большим R получить решение для бесконечной пластины толщины d. Исследовать предельные случаи больших d - полупространство, малых d - тонкая плоскость.
Вот тогда я успокоюсь.
Можно вместо цилиндрической шайбы рассмотреть сплюснутый эллипсоид вращения.
Я не шучу.
Относительно поля в той части, где заряд.
Оно будет в два раза больше исходного поля, поскольку проводящее полупространство вытеснит половину поля, сделает свое нулевым и удвоит бывшее. А если это не полупространство, а полоса конечной ширины?
И два слова об экранировке.
С самого начала нужно определить, что значит внутренняя и внешняя области.
07.01.2016
|
|
|
|
| |
|
|
miflin | Дата: Четверг, 07.01.2016, 14:37 | Сообщение # 362 |
miflin
Ранг: Профессор (?)
Хмырь обыкновенный
Группа: Пользователи
|
| Сообщений: |
2663 |
| Награды: |
87 |
| Статус: |
Offline |
|
Цитата Александр_Игрицкий (  ) Меня может устроить только точное решение уравнения Лапласа для такой задачи.
Вас - да. Не сомневаюсь, что Вы его знаете.
И если изложите так, что оно будет доступно "дотошному школьнику" (не прошедшему параллельно 11-летке ещё
и 5-летний курс физфака универа), то это будет здорово.
07.01.2016
|
|
|
|
| |
|
|
Александр_Игрицкий | Дата: Воскресенье, 10.01.2016, 13:06 | Сообщение # 363 |
| Сообщений: |
11095 |
| Награды: |
129 |
| Статус: |
Offline |
|
miflin, есть предложение ограничиться изложением поведения проводящей плоскости в поле другой проводящей плоскости. Принципиальные моменты, связанные с индуцированными зарядами, остаются, возможная экранировка может проявиться, схема вычислений прозрачная. А что ещё нужно для школьника? Моим словам относительно того, что меня может устроить или не может устроить, присвоим обычный гриф ДСП.
...
А вот несколько задачек вполне для дотошных школьников.
1. Решить уравнение:
|2x-a|=x^2+2a
2. Найти значения параметра "а", при которых все решения уравнения
4|x-3a|+6a-24+x=0
принадлежат интервалу [6;12].
3. Найти минимальные решения уравнения:
x^3+2ax^2-x(a+1)^2=2a(1+a)^2
И ещё одно:
tg(2016pi*sin(pi/(x^2+1))=0
pi - это pi=3.1415...
10.01.2016
Сообщение отредактировал Александр_Игрицкий - Воскресенье, 10.01.2016, 13:46
|
|
|
|
| |
|
|
miflin | Дата: Воскресенье, 10.01.2016, 21:49 | Сообщение # 364 |
miflin
Ранг: Профессор (?)
Хмырь обыкновенный
Группа: Пользователи
|
| Сообщений: |
2663 |
| Награды: |
87 |
| Статус: |
Offline |
|
Цитата Александр_Игрицкий (  ) 3. Найти минимальные решения уравнения:
...
tg(2016pi*sin(pi/(x^2+1))=0
Если минимальное по модулю - 0.
Если с учетом знака - лежит в минус бесконечности.
10.01.2016
|
|
|
|
| |
|
|
Александр_Игрицкий | Дата: Воскресенье, 10.01.2016, 21:53 | Сообщение # 365 |
| Сообщений: |
11095 |
| Награды: |
129 |
| Статус: |
Offline |
|
miflin, и ещё одно - это отдельно. Просто найти все решения.
10.01.2016
|
|
|
|
| |
|
|
miflin | Дата: Воскресенье, 10.01.2016, 22:05 | Сообщение # 366 |
miflin
Ранг: Профессор (?)
Хмырь обыкновенный
Группа: Пользователи
|
| Сообщений: |
2663 |
| Награды: |
87 |
| Статус: |
Offline |
|
Цитата Александр_Игрицкий (  ) Просто найти все решения.
Имеется это в виду?
sin(П/(1+x^2))=n/2016, n=0,1,2...2016
Отсюда выражаем х с учетом, что аргумент синуса лежит в пределах 0..П.
Собственно, это частично учтено в выборе n>=0, а для арксинуса брать два значения -
главное (скажем а) и П-а, ну и плюс-минус перед корнем.
10.01.2016
Сообщение отредактировал miflin - Воскресенье, 10.01.2016, 22:14
|
|
|
|
| |
|
|
Александр_Игрицкий | Дата: Воскресенье, 10.01.2016, 22:43 | Сообщение # 367 |
| Сообщений: |
11095 |
| Награды: |
129 |
| Статус: |
Offline |
|
miflin, немного не так.
3. Найти минимальные решения уравнения:
x^3+2ax^2-x(a+1)^2=2a(1+a)^2
Это отдельное независимое уравнение.
Минимальность нужно понимать так:
при каждом допустимом значении параметра "а" выбрать то решение, какое является минимальным.
...
Уравнение с нагромождением в тангенсе - отдельное.
Здесь нужно найти все решения.
10.01.2016
|
|
|
|
| |
|
|
miflin | Дата: Воскресенье, 10.01.2016, 23:23 | Сообщение # 368 |
miflin
Ранг: Профессор (?)
Хмырь обыкновенный
Группа: Пользователи
|
| Сообщений: |
2663 |
| Награды: |
87 |
| Статус: |
Offline |
|
Цитата Александр_Игрицкий (  ) x^3+2ax^2-x(a+1)^2=2a(1+a)^2
Набросал на скорую руку. Если не ошибся, то так:
1. При а от минус бесконечности до -1: х = а+1.
2. При а от -1 до 1: х = -а-1.
3. При а от 1 до бесконечности: х = -2а.
При а=-1 х= -а-1 = а+1
При а=1 х= -а-1= -2а
10.01.2016
|
|
|
|
| |
|
|
miflin | Дата: Понедельник, 11.01.2016, 03:40 | Сообщение # 369 |
miflin
Ранг: Профессор (?)
Хмырь обыкновенный
Группа: Пользователи
|
| Сообщений: |
2663 |
| Награды: |
87 |
| Статус: |
Offline |
|
Не спится чёто...
То, что я ранее описал словесно (для тангенса с нагромождением).

11.01.2016
Сообщение отредактировал miflin - Понедельник, 11.01.2016, 03:41
|
|
|
|
| |
|
|
Александр_Игрицкий | Дата: Понедельник, 11.01.2016, 13:09 | Сообщение # 370 |
| Сообщений: |
11095 |
| Награды: |
129 |
| Статус: |
Offline |
|
Уважаемые коллеги!
Предлагаю обсудить, как нужно правильно записывать решение следующих уравнений:
1. sinx=1/2
2. 16cosx-15cos2x=17
Есть ли какие-нибудь разумные правила?
Или есть директивы?
Какие?
11.01.2016
|
|
|
|
| |
|
|
miflin | Дата: Понедельник, 11.01.2016, 19:06 | Сообщение # 371 |
miflin
Ранг: Профессор (?)
Хмырь обыкновенный
Группа: Пользователи
|
| Сообщений: |
2663 |
| Награды: |
87 |
| Статус: |
Offline |
|
Александр, а чем вызван вопрос?
Вроде ж существуют стандартные представления для решений. Типа этого.
Если вопрос вызван формой представления моего решения для "тангенса с нагромождениям"  , ,
то я намеренно прибег к такой форме, как мне казалось, для наглядности. 
Можно было ввести ещё одну переменную (k=0,1) и объединить формулы в одну.
Что взять с нематематика... 
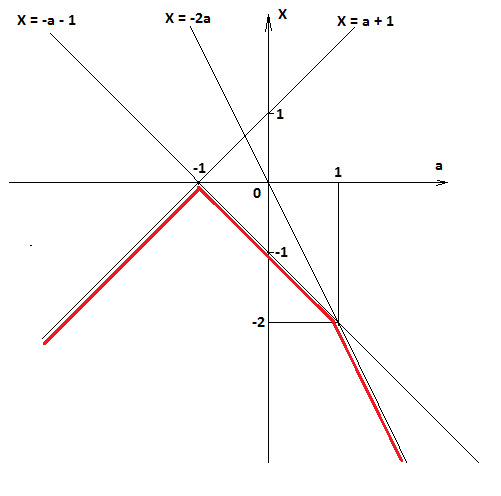
Попутно поясню по уравнению x^3+2ax^2-x(a+1)^2=2a(1+a)^2
Преобразуется к виду (x+2a)(x+a+1)(x-a-1)=0 Имеем 3 прямых x=f(a).
На картинке наглядно видно, что нужно выбирать на интервалах.
11.01.2016
Сообщение отредактировал miflin - Понедельник, 11.01.2016, 19:07
|
|
|
|
| |
|
|
Александр_Игрицкий | Дата: Понедельник, 11.01.2016, 21:54 | Сообщение # 372 |
| Сообщений: |
11095 |
| Награды: |
129 |
| Статус: |
Offline |
|
miflin, Григорий!
Не нужно "ля-ля" про нематематика. Все бы так разбирались!
Про тригонометрию напишу в файле.
Вопрос:
что нужно сделать, чтобы файл был открыт в сообщении, как графики выше?
До сих пор не умею!
11.01.2016
|
|
|
|
| |
|
|
miflin | Дата: Понедельник, 11.01.2016, 22:18 | Сообщение # 373 |
miflin
Ранг: Профессор (?)
Хмырь обыкновенный
Группа: Пользователи
|
| Сообщений: |
2663 |
| Награды: |
87 |
| Статус: |
Offline |
|
Цитата Александр_Игрицкий (  ) что нужно сделать, чтобы файл был открыт в сообщении, как графики выше?
Если файл в формате Word, то ничего не сделать, т.к. в движок форума не встроена программа чтения
вордовских документов, насколько я понимаю.
С графическими объектами проще, т.к. средства чтения графики в движке имеются.
Я цепляю файл-картинку (jpg или png), жму "добавить ответ", потом копирую ссылку на картинку (внизу поста),
вызываю пост на редактирование ("изменить") и через кнопочку "img" вставляю ссылку -
картинка теперь в натуральную величину.
Этого можно и не делать, но тогда читателю приходится открывать картинку в отдельном окне, что не совсем удобно.
Что касается формул, которые я публикую иногда, то я иду на другой форум, где есть ТЕХ, набираю формулу,
потом клавишей PrtSc (Print Screen) загоняю снимок экрана в буфер обмена, в штатном редакторе Paint
делаю "вставить", обрезаю лишнее, и сохраняю в графический файл (только не bmp - он не упакован и чересчур велик),
который потом цепляю к посту. Есть также онлайн-сервисы, в которых набираешь в ТЕХе формулу и сохраняешь её
на свой диск в виде картинки.
11.01.2016
|
|
|
|
| |
|
|
Александр_Игрицкий | Дата: Понедельник, 11.01.2016, 22:36 | Сообщение # 374 |
| Сообщений: |
11095 |
| Награды: |
129 |
| Статус: |
Offline |
|
miflin, понял. Спасибо!
11.01.2016
|
|
|
|
| |
|
|
miflin | Дата: Понедельник, 11.01.2016, 22:46 | Сообщение # 375 |
miflin
Ранг: Профессор (?)
Хмырь обыкновенный
Группа: Пользователи
|
| Сообщений: |
2663 |
| Награды: |
87 |
| Статус: |
Offline |
|
Добавлю, что желательно подцеплять файл в формате doc (Word97-2003), а не docx,
т.к. не у всех последние версии Ворда.
11.01.2016
|
|
|
|
| |
|




 ,
,
