Разработка урока геометрии "Теорема Пифагора"; 8 класс

Автор работы: Монахова Елена Юрьевна

Должность и место работы: учитель математики МКОУ СОШ №1 г. Сортавала Республики Карелия.

Пояснительная записка.

Урок посвящен одной из важнейших теорем планиметрии - теореме Пифагора. Данный урок – это урока открытия новых знаний. На уроке представлена проблемно-поисковая ситуация; рассматривается доказательство теоремы Пифагора и применение ее к решению возникшей проблемы. Учащиеся самостоятельно доказывают теорему. Урок способствует развитию познавательного интереса, навыков самостоятельного пополнения знаний. Усиление практической направленности обучения способствует прочному, неформальному усвоению материала. Урок сопровождается презентацией с исторической справкой и рядом тестовых заданий.

Урок геометрии в 8 классе.

Тема: Теорема Пифагора

Цель урока: Выработать компетенцию по применению теоремы

Пифагора при решении геометрических и практических задач.

Задачи:

1). В процессе учебной деятельности учащихся вывести формулировку и доказательство теоремы Пифагора.

2). Выработать умение учащихся составлять математическую модель реальной ситуации с использованием теоремы Пифагора.

3). Познакомить учащихся с выдающимся математиком, философом и пророком Пифагором.

Ход урока.

1. Самоопределение к деятельности:

Учитель: Ребята, сегодня мне хотелось бы начать урок с задачи.

«Пожарные увидели на крыше горящего дома маленького котенка. Котенок жалобно пищал и звал на помощь. Но вот беда: пожарная машина не может приблизится к дому ближе, чем на 6м, высота дома – 8м. Свою лестницу пожарники могут растянуть не более, чем на 11м. Достаточно ли этого, чтобы помочь бедному котенку?»

Далее необходимо дать ребятам время для решения этой задачи.

Как правило, мнения разные: одни считают, что «да», другие – «нет»

Учитель: сформулируем задачу в общем виде:

Известны катеты прямоугольного треугольника.

Найти длину его гипотенузы

Пока мы не можем решить эту задачу, но к концу урока, применив все свои знания и способности, я надеюсь, что мы сможем помочь нашему маленькому котенку.

2. Актуализация знаний учащихся:

Вопросы классу: - Какие свойства площадей вам известны?

- Площади каких фигур мы можем вычислить?

Решить задачи (устно) с целью подготовки учащихся к восприятию нового материала:

а) Известно, что α = 3β

Найти: β

б) Известно, что α + γ = β

Найти: β

в) По данному рисунку докажите, что

КMNР - квадрат

Какие еще задачи мы можем решить, используя данный чертеж?

(Для удобства ребят можно ввести обозначения: AK=a, AP=b, KP=c)

Наводящие вопросы:

- Какие фигуры вы видите на чертеже?

- Что вы можете сказать о площадях этих фигур?

- Какое свойство площадей здесь можно использовать?

(Путем диалога, арифметических преобразований подвести ребят к

записи: a² + b² = c²).

Вопросы классу:

- Чем являются в нашей ситуации переменные a, b, c?

- Сформулируйте фразу, закодированную в записи a²+b²=c², которая связывает площади наших фигур?

Учитель: Ребята, вы не представляете, что сейчас произошло! Вы сделали величайшее открытие!!! Вы «открыли» теорему Пифагора! Итак, тема нашего урока: «Теорема Пифагора». (Предложить учащимся записать в тетрадях тему урока и ее формулировку).

2. Изучение нового материала: с помощью компьютера рассмотреть только первые два раздела презентации («Теорема Пифагора» и «Проверь себя»).

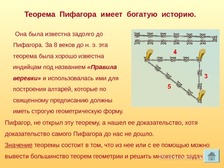
Учитель: Теорема Пифагора – одна из главных теорем геометрии, и можно сказать, самая главная. Значение ее состоит в том, что из нее или с помощью ее можно вывести большинство теорем геометрии.

Теорема Пифагора замечательна еще и тем, что сама по себе она вовсе не очевидна! Например, свойства равнобедренного треугольника можно непосредственно видеть на чертеже. Но сколько ни смотри на прямоугольный треугольник, никак не увидишь, что между его сторонами есть простое соотношение: c²=a²+b²

Зато это соотношение между площадями геометрических фигур становится очевидным из построения на рисунках.

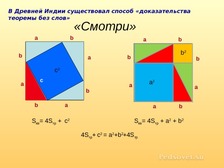
В Древней Индии существовал способ «доказательства теоремы без слов». Слушателям представляли чертеж и писали одно слово «смотри».

Выслушав предположения ребят, сделать вывод: Мы видим два различных разбиения одного и того же квадрата со стороной a+b.

Если из площадей одинаковых квадратов убрать площади одинаковых прямоугольных треугольников, то остаются равные площади: c²=a²+b².

В этом состоит самый лучший математический стиль: посредством остроумного построения сделать неочевидное очевидным.

3. Закрепление изученного материала:

Учитель: Ребята, наш котенок по-прежнему ждет вашей помощи. Давайте вернемся к нашей задаче.

Дано: _∆ АВС, ےВ = 90⁰

Найти: АС

Решение: _Δ АВС – прямоугольный

По теореме Пифагора АС²=АВ²+ВС² ═>

АС²= 6²+8² – это математическая модель

данной ситуации.

АС² = 100, АС = 10

Ответ: 10 м до крыши, т.е. лестницы

вполне достаточно.

Задача №2: Египтяне придумали задачу о лотосе: «На глубине 12 футов растет лотос с 13 футовым стеблем. Определите, на какое расстояние цветок может отклониться от вертикали, проходящей через точку крепления стебля ко дну».

Дано: _∆ АВС , ےС = 90⁰, АВ = 13м, АС=12м

Найти: ВС

Решение: _∆ АВС – прямоугольный, т.е. по

теореме Пифагора имеем: АВ²=АС²+ВС²

а значит ВС² = АВ² - АС²

ВС² = 13² - 12², ВС² = 25 ═> ВС = 5

Ответ: 5 футов.

Задача №3: Дерево в 8м высотой переломлено бурей так, что если верхнюю часть пригнуть к земле, то верхушка коснется земли на расстоянии 4м от основания ствола. На какой высоте переломлен ствол?

Решение: И вновь при составлении математической

модели мы используем теорему Пифагора:

(8 - х)² = х² + 4²

64 – 16х + х² = х² + 16

16х = 48 х = 3

Ответ: 3м

4. Самостоятельное решение задачи:

I уровень – Коробка конфет имеет форму равнобедренного треугольника, боковая сторона которой равна 25см, а основание – 14см. Какова высота этой коробки? (Ответ: 24см)

II уровень – Цветочная клумба имеет форму равнобедренной трапеции с основаниями10 и 18 см, и с боковой стороной равной 5см. Найти площадь клумбы. (Ответ: 42см²)

Учитель: - Возможно ли было решение задач данного типа без знания

теоремы Пифагора?

- В чем суть теоремы Пифагора?

- О чем надо помнить, применяя теорему Пифагора?

5. Историческая справка:

Закончить просмотр презентации «Теорема Пифагора».

6. Подведение итогов урока:

Учитель: Сегодня мы с вами познакомились с теоремой Пифагора. Вы согласны с тем, что это одна из важнейших теорем геометрии? Почему? Теорема Пифагора справедлива только для прямоугольных треугольников. Так ли уж часто мы имеем с ними дело?

Объявить оценки.

Домашнее задание: I группа - №484б, 486 II группа - №488 а,б