Психолого-педагогические и дидактико-методические особенности обучения учащихся стереометрии
Четыре формы движения познания учащихся
Советские психологи (В.Н. Мясищев, А.Г. Ковалев, И.С. Якиманская и др.) рассматривают умения в качестве одного из критериев развития способностей. Формируя определенное умение, развивая интеллект ученика, его способности, учитель формирует и личностные качества обучающегося, такие, как внимательность, настойчивость, инициативность, трудолюбие и др. Таким образом, формирование умений способствует становлению и развитию личности, готовит учащихся к трудовой деятельности в различных сферах.
Несмотря на определенные успехи в теоретической и практической разработке вопроса о путях формирования умений учащихся, необходимых для решения задач, эти умения, как мы уже отмечали, у многих учащихся находятся на низком уровне сформированности.
Помимо уже отмеченных причин, лежащих в основе неумения учащихся решать задачи, и, в частности, стереометрические, следует также отметить и то обстоятельство, что в методической литературе, в практике работы учителей математики не уделяется должного внимания разработанным психологами и дидактами (С.Л. Рубинштейном, Н.А. Менчинской, Е.Н. Кабановой-Меллер, М.Н. Скаткиным, А.М. Даниловым, В.А. Онищуком и др.) теоретическим основам формирования навыков и умений. Исследованные общие закономерности формирования навыков и умений еще на нашли должной конкретизации в работах по методике изучения наиболее сложных разделов школьного курса математики. Мало работ, в которых с должной полнотой разрабатывались бы конкретные вопросы методики формирования общеучебных умений, умений по решению стереометрических задач, организации совместной деятельности учителя и ученика в процессе работы по формированию умений, необходимых для решения задач.
Чтобы оказать дифференцированную помощь учащимся в ходе поиска решения каждой конкретной задачи, следует определить уровень сформированности умений учащихся по решению геометрических задач.
Знание уровня сформированности у школьников навыков и умений по решению задач, позволяет спланировать все виды дифференцированных воздействий, подобрать соответствующие задачи и продумать формы помощи для различных групп учащихся, ориентируясь при этом на зону их ближайшего развития.
При организации учебного процесса по обучению учащихся решению задач, в том числе и стереометрических, читателю следует напомнить, что существуют четыре формы движения познания учащихся в этом процессе:
- от одних чувственных образов к другим (чувственное познание);
- от одних понятий к другим (логическое познание);
- от образов к понятиям (взаимодействие чувственного и логического познания);
- от понятий к образам (взаимодействие логического и чувственного познания).
Заметим, что формы в) и г) психологи относят к интуитивному познанию. Включение в курс стереометрии задач, решаемых на уровне интуитивного познания, и определенным образом организованная работа над ними, способствуют развитию логического и пространственного мышления.
Высказанное положение подчеркивает тот факт, что хотя логика и пронизывает весь школьный курс стереометрии, но не она одна должна доминировать в разработке методики обучения учащихся стереометрии.
А.Д. Александров подчеркивал: «Во всяком подлинно геометрическом предложении, будь то аксиома, теорема или определение, неразрывно присутствуют два элемента: наглядная картина и строгая формулировка, строгий логический вывод. Там, где нет одного из них, нет и подлинной геометрии. В этом и состоит, — продолжает ученый, — в конечном счете, противоречие в сущности геометрии, в ней непосредственно изучаются идеальные геометрические фигуры, которых нет в действительности, но ее выводы применяются к реальным вещам, к практическим задачам. Так оно происходит и в школьном преподавании: аксиомы, определения, теоремы относятся к идеальным фигурам, но поясняются на реальных примерах и применяются в решении реальных задач… Наглядность входит в доказательства и определения, которые в свою очередь придают наглядности большую точность».
Из сказанного следует, что раз стереометрия соединяет в себе наглядную картину, модель и строгую формулировку, то в основу методики ее обучения должен быть положен наглядно-конструктивный подход. Заострить это положение можно высказыванием того же А.Д. Александрова.
Этот крупнейший геометр ХХ века, зная все тонкости своей науки, давал такой совет тем, то начинает изучать стереометрию: «Основное правило состоит в том, что, встречаясь с определением, теоремой или задачей, нужно прежде всего представить и понять их содержание: представить наглядно, нарисовать или, еще лучше, хотя и труднее, вообразить то, о чем идет речь, и одновременно понять, как это точно выражается. Ничего не старайся заучить, не нарисовав, не вообразив того, о чем идет речь, не поняв, как это наглядное представление выражается в формулировке определения, теоремы или задачи».
Другой ученый, также знающий толк в математике и в методикеее преподавания, В.И. Арнольд, отмечает: «Выхолощенное и формализованное преподавание математики на всех уровнях сделалось, к несчастью, системой. Наиболее характерными приметами формализованного преподавания является изобилие немотивированных определений и непонятных (хотя логически безупречных) доказательств. Отсутствие примеров, отсутствие анализа чертежей и рисунков столь же постоянный недостаток математических текстов, как и отсутствие внематических приложений и мотивировок понятий математики».
Основная суть наглядно-конструктивного метода обучения стереометрии состоит в том, что теоретические знания имеют в своей основе чувственность предметно-практической деятельности. Для ученика это означает учебную предметно-практическую деятельность по созданию различных моделей стереометрических объектов.
Говоря о роли деятельности в познании, А.Н. Леонтьев отмечал: «Чтобы овладеть предметом или явлением, нужно активно осуществить деятельность, адекватную той, которая воплощена в данном предмете или явлении».
Итак, подчеркнем еще раз, что субъектом учебной предметно-практической деятельности является ученик, а объектом– модель, создаваемая им, причем акцент ставится на познании этой модели. В таком случае не чувственность созерцания, а чувственность учебной предметно-практической деятельности является истоком понятийного знания; эта деятельность, сопровождаемая построением и преобразованием модели, позволяет выделить генетически исходное начало, некоторое всеобщее начало. «Благодаря такой особенности чувственности учебной предметно-практической деятельности, — отмечает
Г.П. Сенников, — возникает наглядно-действенная форма теоретического мышления, становится возможным переход к абстрактным (но овеществленным) теоретическим понятиям, то есть переход на ступень рационального знания».
Модели, используемые в обучении, могут быть самые различные.
Например, моделями понятия пирамиды могут быть:
- словесное описание (определение) этого понятия;
- объемная модель пирамиды (каркасная, сплошная);
- ее развертка;
- изображение пирамиды или ее развертки на доске, на бумаге, на экране и т.п.
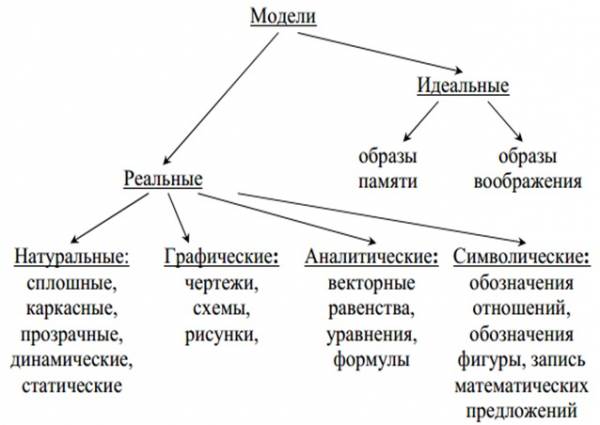
Модели, используемые в процессе обучения учащихся стереометрии, можно классифицировать следующим образом.
Следует, конечно, заметить, что оперирование реальными и идеальными моделями есть единый процесс. Причем, некоторый объект В становится моделью оригинала А лишь в том случае, если В есть продукт гностической деятельности субъекта К или объект В есть объект исследования в этой деятельности.
Процесс моделирования можно описать как особую деятельность субъекта по построению или выбору модели в связи с поставленными познавательными целями.
Приведем, пусть и неполный, перечень наглядных средств, которые можно использовать в процессе обучения учащихся стереометрии.
Важнейшей задачей школьного математического образования является задача формирования и развития у учащихся мышления вообще и математического в частности. Эта задача напрямую связана с решением проблемы вооружения учащихся математическими видами деятельности.
Известно, что процесс усвоения содержания науки в своей основе происходит с помощью тех же форм мышления, что и его развитие.
Показательны в этом плане слова Д. Брунера: "Умственная деятельность везде является той же самой, на переднем ли фронте науки, или в третьем классе школы. Деятельность ученого за его письменным столом или в лаборатории, деятельность литературного критика при чтении поэмы — это деятельность того же порядка, что и деятельность любого человека, когда тот занят подобными вещами, если перед ним стоит задача достигнуть понимания определенных явлений. Различие здесь в степени, а не в роде".
Процесс создания математических знаний подобен созданию любых других человеческих знаний, и он в значительной степени строится на переносе отношений и свойств из одной системы в другую систему. Последнее есть определяющая черта тех форм мысли, которые носят название выводов по аналогии. За счет этих выводов по аналогии, которые позволяют переносить результаты, полученные в одной области, на другие области, происходит увеличение этих результатов.
В плане нашей работы значимо высказывание И. Кеплера: "И я больше всего дорожу Аналогиями, моими самыми верными учителями. Они знают все секреты Природы, и ими меньше всего следует пренебрегать в Геометрии".
Итак, перенос знаний, полученных при изучении одного объекта на другие объекты, — важнейшая задача не только развития науки, но и школьного образования.
Центральным видом учебной деятельности, в процессе которой учащимися усваивается математическая теория, развиваются самостоятельность мышления и их творческие способности, является решение задач. Низкий уровень творческого мышления, встречающийся в знаниях учащихся, формализм и отсутствие должной самостоятельности при поиске решения задач, есть следствие несовершенства методики обучения школьников решению задач.
Наибольшие трудности испытывают учащиеся при решении стереометрических задач, ибо для их решения, роме прочих знаний по планиметрии и стереометрии, необходимо уметь рационально выбирать нужные теоретические знания, уметь применять большое разнообразие приемов поиска решения и соединять в процессе решения одной задачи различные математические методы.
Как показывает проведенный нами педагогический эксперимент, эффективным методом обучения учащихся решению стереометрических задач является метод аналогии, так как именно аналогия чаще всего лежит в начале поиска решения многих задач стереометрии. Формирование у учащихся умения применять метод аналогии следует рассматривать как один из эффективных путей развития творческой активности школьников.
Ряд отечественных и зарубежных ученых Д. Пойа, Ю.М. Колягин, А.А. Столяр, Л.М. Фридман, А.И. Уемов, Г.Д. Балк, А.И. Жохов, Б.З. Хынг, Р.Ю. Костюченко и др., в своих работах обращались к рассмотрению вопроса об аналогиях. Ими получены следующие результаты и выводы:
- аналогия — особая форма мысли, в результате которой информация одного сложного объекта (модели) переносится на другой (оригинал);
- аналогию целесообразно использовать на различных этапах процесса обучения математике: при повторении материала, для установления связей между различными темами курса, при отыскании решения некоторых задач;
- применение аналогии в обучении развивает творческие способности учащихся, а степень овладения аналогией характеризует уровень творческого развития человека;
- дети с первых шагов познания мира, а также в процессе учения стихийно пользуются аналогией;
- аналогия приучает учащихся к исследовательской деятельности;
- аналогия облегчает усвоение школьниками учебного материала, так как позволяет осуществить мысленный перенос определенной системы знаний, умений и навыков от известного объекта к неизвестному;
- метод аналогии лишь тогда становится эффективным средством обучения учащихся, когда последние не спонтанно, а целенаправленно были вооружены знаниями об аналогии и у них были выработаны умения использовать метод аналогий;
- аналогия обеспечивает живость и полноту изложения учебного материала, а также прочность запоминания этого материала;
- если в процессе обучения отсутствует аналогия, то знания теряют стадию недосказанного, предполагаемого, хотя известно, что прежде всего нужно догадаться о математическом факте, а только потом его доказывать; нужно прежде всего догадаться об идее доказательства, а затем уже проводить его в деталях (согласно требованиям историзма, истина должна проходить через стадию проблемности);
- в психологии установлено, что человек лучше запоминает то действие, которое осталось незавершенным, а аналогия, в отличие от дедукции, позволяет обеспечить остаточную напряженность, которая возникает в результате переноса информации с одного объекта на другой и отсутствия при этом доказательности выдвигаемых гипотез и предположений;
- аналогия позволяет оставить некоторые задачи незавершенными, что вызывает у учащихся интерес и стимулирует их учебно-познавательную деятельность;
- выводы по аналогии позволяют уменьшить степень схематизации и идеализации действительности и обучают учащихся проводить, в отличие от логических умозаключений, еще и рациональные умозаключения, основанные на здравом смысле;
- аналогия содействует появлению новых ассоциаций, которые способствуют углубленному, более сознательному пониманию материала, качественному обновлению знаний;
- знания, приобретенные отдельно друг от друга, посредством аналогии соединяются воедино, а значит, аналогия способствует систематизации знаний и рациональному их запоминанию.
Несмотря на большую эффективность метода аналогии в учебном процессе, учителя не владеют методикой обучения учащихся этому методу, да и в дидактико-методической литературе отсутствует необходимое описание обучающей деятельности учителя и учебно-познавательной деятельности учащихся в процессе использования аналогии, пока нет полных ответов на вопросы: "Где и как использовать аналогию?", "Какие существуют пути и средства формирования у учащихся умения использовать аналогию?", не выявлены общие закономерности использования метода аналогии и приемы его применения. В философской, математической, психолого-педагогической и методической литературе отсутствует единый подход к определению понятия аналогии.
Рассмотрим некоторые подходы исследователей к определению аналогии.
- Аналогия как понятие, выражающее отношение сходства между различными объектами, системами, явлениями, процессами.
- Аналогия как эвристический метод научного познания и как средство переноса информации из одной области в другую.
- Аналогия как особая логическая форма умозаключения, как один из методов рассуждения.
В литературе чаще всего аналогию трактуют в отмеченном выше первом понимании и тогда она есть характеристика глубокого внутреннего сходства, одинаковости структуры множеств предметов различной природы. Сходство объектов, которые принадлежат различным классам, проявляется в общности некоторых или всех существенных свойств этих объектов. Термин "аналогия" происходит от греческого слова "analogia", что означает "соответствие". Сложный объект Х аналогичен сложному объекту У относительно набора Р характеристик, если в Р найдется хотя бы одна характеристика, общая для Х и У.
Обычная схема умозаключения по аналогии: объект Х обладает признаками a, b, c, d, e, объект У обладает признаками b, c, d, e, следовательно, объект У, вероятно, обладает признаком а.
Приведем примеры аналогий планиметрических и стереометрических фактов.
- Устанавливается связь по аналогии между треугольниками и тетраэдрами, между окружностью и сферой и т.д. В планиметрии известен факт: "В любой треугольник можно вписать единственную окружность, центр которой находится на пересечении геометрических мест точек, равноудаленных от сторон треугольника". Находя аналогию между простейшим многоугольником — треугольником и простейшим многогранником — тетраэдром, мы строим следующее умозаключение по аналогии: "В любой тетраэдр можно вписать единственную сферу, центр которой находится на пересечении геометрических мест точек, равноудаленных от граней тетраэдра". Конечно, это утверждение требует своего дедуктивного доказательства, которое строится на синтезе понятий и их свойств, относящихся к тетраэдру, причем этот синтез строится в том же порядке, в каком он проводился и для треугольников.
- Плоскостная изопериметрическая теорема — пространственная изопериметрическая теорема.
Об авторе: Зловидова Ирина Анатольевна, магистрант 2 курса ОмГПУ г. Омска факультет математического образования.