Применение геометрии в общетехнических и специальных предметах колледжа
Чебоксарский электромеханический колледж — победитель федерального конкурса-эксперимента по реализации программ прикладного бакалавриата. Программа прикладного бакалавриата приравнена к высшему образованию. Она сочетает в себе практическую подготовку, характерную для техникумов, и теоретическую, свойственную вузовскому бакалавриату.
Бакалавр — это универсальный специалист, востребованный экономикой, который будет уметь делать многое своими руками и при этом обладать академическим мышлением. Он сможет самостоятельно проектировать, руководить и организовывать работу.
Таким образом, важнейшей задачей нашего колледжа является преподавание дисциплин, в том числе и математики, на основе активизации творческой деятельности обучающихся с учетом профессиональной направленности. Для этого необходимо осуществление межпредметных связей. Заинтересовать студентов, сделать предмет математики для них нужным и актуальным есть цель работы педагога.
Для достижения данных целей мы решили создать блок рабочих тетрадей (РТ) для самостоятельной работы студентов, в которых отразили взаимосвязь математики и спецдисциплин. В частности в данной статье рассмотрим структуру рабочей тетради «Векторы и координаты». Различные связи указанной темы с общетехническими и специальными предметами можно выявить в ее взаимодействии с технической механикой. Также имеются свои особенности использования векторов и метода координат в физике, ТОЭ и других предметах.
При составлении РТ «Векторы и метод координат» был сделан акцент на личностное развитие студентов; чтобы она дала возможность работать со студентами различной степени подготовленности, разного уровня развития.
РТ включила вопросы и задания следующих групп:
- на воспроизведение изученного материала;
- для развития мыслительных операций;
- для практического применения полученных теоретических знаний;
- задачи разного уровня сложности;
- задания и свободное место для самостоятельной работы.
В тетради помещены алгоритмы решения геометрических задач, формулы и таблицы для самостоятельного заполнения. Работа в данной тетради может быть выполнена в электронном виде, поскольку многие студенты в процессе обучения используют современные средства: ноутбуки, электронные книги, айпады и т.д. Проверка контрольных срезов, включенных в РТ, может быть осуществлена по электронной почте, на форуме студентов колледжа.
Итак, структура и содержание РТ «Векторы и метод координат» определена следующим образом:
- Информационный комплекс по каждому разделу темы: краткие исторические сведения, краткие теоретические сведения с пропущенными данными для самостоятельного заполнения, алгоритм решения типовых примеров.
- Задачи и упражнения для самостоятельной работы студентов: типовые, развивающие и творческие упражнения.
- Обобщение и заключение по каждому разделу темы: применение раздела в специальных дисциплинах (межпредметные связи), вопросы, творческие задания для ВСР (внеаудиторной самостоятельной работы), контрольный срез.
Контрольный срез осуществляется с помощью гиперссылки на большое количество вариантов заданий.
Рассмотрим более подробно межпредметные связи, указанные в каждом разделе тетради.
Раздел 1. Векторные величины.
Математической моделью векторной величины является вектор. Наиболее важный пример векторной величины в общетехнических курсах – сила, изображенная направленным отрезком. Если силе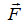 
на чертеже соответствует отрезок длиной l, то ее масштабом будет 
.
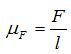Размерность масштаба вектора получается делением размерности модуля векторной величины 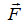на размерность длины l.
В технической механике совокупность сил, одновременно действующих на какое-либо тело, называется системой сил: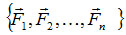 
.
Классификацию сил, их свойства изучает статика – один из разделов технической механики. Важнейшей аксиомой статики является правило параллелограмма: равнодействующая двух сил, приложенных в одной точке, приложена в той же точке и изображается диагональю параллелограмма, построенного на данных силах.
Другой раздел технической механики – кинематика, где векторными величинами являются скорость и ускорение материальной точки. А специфическими векторными величинами динамики являются сила, ускорение и количество движения (импульс).
В электродинамике и электротехнике для описания процессов используются такие векторные величины, как сила и плотность тока.
Раздел 2. Действия над векторами.
В технической механике используют правила параллелограмма и треугольника. Так, модуль равнодействующей силы может быть найден двумя методами: графическим и графоаналитическим. При графическом решении статистической задачи данные силы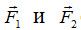 
и откладываются на чертеже в выбранном масштабе. Затем, построив параллелограмм или треугольник сил, получают величину равнодействующей в данном масштабе. Этот метод широко применяется в графостатике, рассматривающей графическое решение задач.
При графоаналитическом методе достаточно знать угол альфа между данными силами и их модули 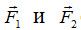и , чтобы по теореме косинусов получить модуль равнодействующей:
.
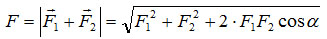Геометрическая сумма – главный вектор любой системы сил в графостатике определяется или последовательным сложением сил по правилу параллелограмма, или построением силового многоугольника, что считается более простым и удобным [3,4].
Раздел 3. Координаты точек и векторов.
В общетехнических курсах говорят не о координатах точек или векторов, а об их проекциях. Например, в статике основания перпендикуляров, опущенных из данных точек на ось, называют проекциями этих точек на данную ось. Длину отрезка оси, заключенного между проекциями на ось начала и конца отрезка, изображающего данный вектор, взятую с соответствующим знаком, называют проекцией этого вектора на ось.
В механике геометрически показывают, что проекция вектора на ось равна модулю этого вектора, умноженному на косинус угла между вектором и положительным направлением оси, а модуль вектора равен квадратному корню из суммы квадратов его проекций на две взаимно перпендикулярные оси, в плоскости которых лежит данный вектор.
В статике одним из узловых является вопрос о центре тяжести тела. Вначале определяют центр параллельных сил, сославшись на формулу для координат точки, делящий отрезок в данном отношении m/n, из геометрии:
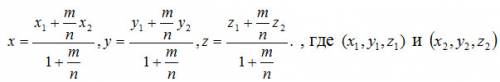, где и — координаты концов данного отрезка. Затем, зная правила сложения двух параллельных сил, последовательным сложением находят равнодействующую и для любой системы параллельных сил.
Метод координат позволяет также аналитически найти равнодействующую плоской и пространственной систем сходящихся сил, вывести условия равновесия, определить модуль и направление главного вектора. Это делается на основе теоремы о проекции геометрической суммы векторов на ось [3,4].
Раздел 4. Уравнения линий.
В общетехнических курсах понятие линии ассоциируется с понятием траектории движения.
В кинематике под траекторией движения понимают геометрическое место положений движущейся точки в рассматриваемой системе отсчета. Движение точки называют прямолинейным, если ее траектория – прямая линия, и криволинейным, если ее траектория – кривая линия. С физической точки зрения движения точки (тела) могут быть равномерным и неравномерным.
Движение точки задается естественным или координатным способами. При естественном способе задания движения точки должны быть известны: траектория точки в выбранной системе отсчета; начало отсчета и направление движения точки на кривой; закон движения точки по данной траектории в виде уравнения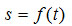 
или графика.
При координатном способе задания движения под уравнениями движения точки в прямоугольных координатах понимаются уравнения, выражающие зависимость координат точки от времени в процессе движения:
.
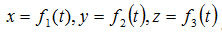Наиболее важной функциональной зависимостью в общетехнических курсах является линейная зависимость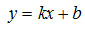 
, графическим образом которой является прямая линия, например, закон Ома [2].
При изучении молекулярной физики студенты знакомятся с процессами, происходящими в идеальном газе [2]. Изохорный процесс иллюстрируется графиками-изохорами линейной зависимости давления от температуры. Прямые, изображающие линейную зависимость при изобарном процессе, называют изобарами. А графиком изотермического процесса является ветвь гиперболы.
Таким образом, показанные сведения в рабочей тетради о применении каждого раздела данной темы помогают показать практическую направленность при изучении курса математики, делают понятнее, доступнее, способствуют преодолению формализма в приобретении знаний, развивают умение замечать математические закономерности в окружающем нас мире.
Литература:
- Бродский Я.С. и др. методические рекомендации по математике. Выпуск11. – Москва «Высшая школа», 1989.
- Жданов Л.С., Жданов Г.Л. Физика для средних специальных учебных заведений: Учебник. – М.: Наука, 1984.
- Никитин Е.М. Теоретическая механика для техникумов. – М.: Наука, 1983.
- Портаев Л.П. и др. Техническая механика: Учебник для техникумов. – М.: Стройиздат, 1987.
Об авторе: Ситникова Марина Анатольевна, преподаватель математики, "Чебоксарский электромеханический колледж" Министерства образования Чувашии.
