Разбор некоторых типовых заданий олимпиады по программированию
Если сравнить количество участников олимпиад по математике, физике с количеством участников олимпиады по программированию, то получается следующее: нг математику приходит в среднем 200 участников, на программирование — 50, что в четыре раза меньше. Возникает вопрос: ПОЧЕМУ? Давайте попробуем разобраться.
Все задачи, которые предлагаются на олимпиадах по программированию, можно разбить на следующие темы:
- Алгоритмы обработки массивов.
- Длинная арифметика.
- Комбинаторные алгоритмы
- Динамическое программирование.
- Алгоритмы на графах.
- Прочие (вычислительная геометрия, физика, биология, химия)
Для примера рассмотрим задачи районного тура олимпиады 2009-2010 учебного года из раздела алгоритмы обработки массивов.
Задача А: Муравьи
Имя входного файла: ants.in
Имя выходного файла: ants.out
Ограничение по времени: 2 сек
Ограничение по памяти: 64 Мбайт
N муравьев в момент времени 0 начинают одновременно двигаться по горизонтальному отрезку прямой со скоростью 1 см в секунду в заданных направлениях. Если два муравья сталкиваются, то они мгновенно разворачиваются и двигаются с прежней скоростью в противоположном направлении. Муравей, дошедший до края отрезка, падает. Определите, через сколько секунд упадет последний муравей.
Формат входных данных
На первой строке входного файла дано 2 целых числа:
N — количество муравьев (1<=N<=105)
L — длина отрезка в сантиметрах (2<=L<=106).
На второй строке расположены N чисел. I-е число — расстояние в сантиметрах от левого края отрезка до i-го муравья (расстояние — целое число в промежутке от 1 до L-1). Третья строка также содержит N чисел. I-е число равно 0, если i-й муравей начинает двигаться влево и равно 1, если вправо. Числа в строках разделены пробелами.
Формат выходных данных
На единственной строке выходного файла выведите одно целое число — ответ к задаче.
Все задания используют входные и выходные файлы, поэтому нужно очень внимательно просмотреть имена этих файлов.
Решение:
Задача про муравьев относится к разделу "Работа с массивами". Массив значений формируем при считывании данных. Это зависит от значений в третьей строке входного файла, поэтому при считывании данных нужно или оставлять заданное значение, или отнимать от длины отрезка расстояние. Все наши муравьи двигаются с одинаковой скоростью. Поэтому при развороте на 180° муравей пройдет такое же расстояние, что и без разворота. Следовательно, в данной задаче достаточно найти наибольшее значение расстояния от края до муравья, и это будет ответом задачи.
Алгоритм решения задачи:
- Считать исходные данные: количество муравьев и длину отрезка.
- Проверить на ОДЗ исходные данные, согласно формату входных данных.
- Если исходные данные входят в ОДЗ, то выполняем п. 5, иначе — п.4.
- Вывести в выходном файле сообщение "Неверный формат входных данных".
- Формируем первую строку массива расстояний*.
- Формируем вторую строку массива расстояний*.
- Если значение второй строки равно 1, то изменяем значение массива первой строки на разность между длиной отрезка и заданным расстоянием от левого края до муравья.
- Находим максимальное значение в первой строке массива расстояний, это и будет ответ задачи.
- Полученное значение записываем в выходной файл.
* Можно сформировать структуру записи из 2-х полей.
Максимальное значение в первой строке массива расстояний записываем в выходной файл.
Размер массива расстояний задаем в зависимости от максимальных входных данных. Так же задаем типы исходных данных, от этого зависит объем занимаемой памяти. Массив расстояний и длина отрезка типа LongInt, а для записи 0 или 1 можно задать перечисляемый тип данных. Нам еще понадобятся дополнительные переменные это максимальное значение типа LongInt, и переменные для индексов массива.
Задача В: Велосипедист.
Имя входного файла: biker.in
Имя выходного файла: biker.out
Ограничение по времени: 2 сек
Ограничение по памяти: 64 Мбайт
Велосипедист измеряет свою мгновенную скорость раз в минуту, всего N раз. Измерение проводится в начале каждой минуты. Зная результаты измерений, найдите его среднюю скорость за время, прошедшее от первого до последнего измерения. Считайте, что между моментами измерений скорость изменяется строго равномерно. Для справки: средняя скорость — это расстояние, деленное на время, за которое это расстояние было пройдено.
Формат входных данных
На первой строке входного файла дано целое число N — количество замеров (1<=N<=105). На второй строке расположены N чисел: i-е число — мгновенная скорость велосипедиста в начале i-й минуты (в метрах в секунду). Скорости — целые числа в промежутке от 0 до 100. Числа в строке разделены пробелами.
Формат выходных данных
На единственной строке выходного файла выведите одно вещественное число, округленное до двух знаков после десятичной точки — ответ к задаче в метрах в секунду.
Решение:
Основная сложность этой задачи заключается в знании формул равноускоренного движения. При считывании формируем массив исходных данных: начальные скорости на момент времени. Обратите внимание, время задается в минутах, нужно его перевести в секунды.
Для вычисления расстояния при равноускоренном движении используются следующие формулы:
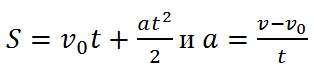
где:
V0 — скорость на начало момента времени, согласно условию задачи на начало минуты,
V — на конец минуты.
Если преобразовать формулу вычисления расстояния при равноускоренном движении, то получим:
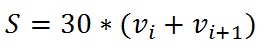
за одну минуту. i изменяется от 1 до n, для вычисления средней скорости, общее расстояние делим на n.
Алгоритм решения задачи:
- Считать исходные данные и проверить их на ОДЗ согласно формату входных данных.
- Сформировать массив скоростей.
- Вычислить расстояние.
- Вычислить среднюю скорость.
Список использованной литературы
- Андреева Е.В. (2009). Программирование — это так просто, програамирование — это так сложно. Москва: Издательство МЦНТМО.
- Окулов С. (2002). Основы программирования. Москва: Лаборатория Базовых Знаний.
- Попов В.Б. (2002). TURBO PASCAL для школьников. Москва: Финансы и статистика.
- У.Болл, Г. (1986). Математические эссе и развлечения. Москва: МИР.
Об авторе: Лариса Алексеевна Пак, учитель информатики, кГУ "Школа-лицей №90" г. Алматы.
0
