Восемь форм группового обучения учеников: одна голова хорошо, а две лучше

• в результате постоянного повторения упражнений совершенствуются навыки логического мышления и понимания;
• дети учатся обсуждать, спорить, отстаивать свою точку зрения, учитывать мнение других;
• каждый чувствует себя раскованно, работает в индивидуальном темпе;
• повышается ответственность не только за свои успехи, но и за результаты коллективного труда;
• обсуждение одной информации с несколькими одноклассниками обеспечивает более прочное усвоение.

Существует много разновидностей групповой формы работы.

Обучение в командах

Схема реализации этого метода может быть представлена следующим образом: в начале урока учитель дает обзорную лекцию по новому материалу с акцентом на тех моментах, по которым команды будут выполнять индивидуальные задания. Лекция должна быть достаточно емкой по содержанию и одновременно практически-направленной. Рекомендуется использование наглядности, моделирования и учебных экспериментов.

Далее учащиеся работают в командах над конспектами лекции, помогая друг другу понять ее содержание. Учащиеся могут задавать друг другу вопросы, проясняя непонятные для себя моменты. Вопросы учителю разрешается задавать только тогда, когда никто из членов команды не может ответить на них. После проработки конспекта лекции учащиеся выполняют индивидуальные работы. На данном этапе помощь друг другу исключается, каждый член команды работает самостоятельно. Главная особенность данного метода заключается в системе оценки индивидуальных работ. Оценка осуществляется по прогрессивно-сравнительному признаку: учащийся может пополнить копилку команды только в том случае, если его оценка за данную работу выше средней его оценки за предыдущие работы. Команда, набравшая по итогам изучения темы наибольшее количество баллов, считается победившей: она заслуживает поощрения и внесения на специальную доску победителей.

Метод учебного турнира

Основная характеристика этого метода заключается в том, что после изучения нового материала в турнирном поединке встречаются учащиеся из разных команд с одинаковым уровнем учебных достижений. Как правило, такого рода турниры проводятся раз в неделю после изучения крупной учебной темы. Порядок проведения таков. Учащиеся из разных команд распределяются по уровню учебных достижений: сильные – первая подгруппа, средние – вторая подгруппа, слабые – третья подгруппа. Каждая подгруппа получает около тридцати пронумерованных карточек с вопросами, расположенных на столе в произвольном порядке в перевернутом виде. Каждый учащийся подгруппы поочередно выбирает карточку и отвечает на вопрос, записанный на ней. Отвечать можно как устно, так и письменно. Остальные члены подгруппы оценивают ответ, к примеру – по альтернативной шкале: правильно (1 балл) и неправильно (0 баллов). В случае спорной ситуации учащиеся прибегают к помощи учителя. В среднем на каждого учащегося приходится по три карточки. Таким образом, учителю необходимо подготовить к турниру около 90 карточек-вопросов трех уровней сложности. После турнира в подгруппах учащиеся возвращаются в свои команды и суммируют полученные баллы. Команда, набравшая наибольшее количество баллов, признается победительницей.

Метод командной поддержки индивидуального обучения

Суть этого метода заключается в предоставлении малым группам возможности продвигаться по учебной программе в индивидуальном темпе. Учащиеся работают в малых группах над индивидуальными заданиями, в процессе выполнения которых они могут обращаться друг к другу за советом, помощью и консультацией. Учащиеся также могут проверять работы друг у друга, помогать исправлять допущенные ошибки. Учитель, в свою очередь, наблюдает за работой групп, а также поочередно разъясняет новый учебный материал группам, которые закончили работать над индивидуальными заданиями по предыдущему материалу. Индивидуальные задания проверяются специально назначенными учителем учащимися – «мониторами» из разных групп. Они снабжаются листами-ответами для оперативной проверки индивидуальных работ. В это время учитель имеет возможность индивидуально работать с каждой малой группой. В конце недели подводится итог: сколько тем изучила каждая группа и каков суммарный учебный результат группы по индивидуальным заданиям.

Метод «американской мозаики» (Jigsaw)

Этот метод  реализуется по следующей схеме: команды формируются по 4–6 человек. Новый учебный материал делится на 4–6 частей, которые распределяются между членами команды, и каждый учащийся самостоятельно изучает свою часть. Затем члены разных команд, изучавшие одинаковую часть учебного материала, собираются вместе для 10–15-минутного обсуждения. После этого они возвращаются в свои команды, и каждый из них поочередно (согласно логике учебного материала) объясняет содержание своей части остальным членам команды. Уровень усвоения учебного материала каждым учащимся оценивается по результатам индивидуальной самостоятельной работы по всему новому материалу. Выигрывает та команда, которая набирает таким образом наибольший балл.

Метод кооперативного взаимообучения

Заключается в постоянной взаимопомощи и взаимоподдержке учащихся посредством взаимопроверок самостоятельных работ, совместного выполнения домашних заданий, пересказа друг другу изучаемого материала, взаимоисправления ошибок, совместной подготовки к зачетам и экзаменам и т.д. Данный метод может применяться в работе различных по форме учебных групп: формальных (сформированных по специальным критериям для решения конкретной учебной задачи), неформальных (укомплектованных по принципу симпатии или дружбы или просто по «территориальному принципу» – сидят за одной партой), базовых (сформированных для решения долгосрочных учебных задач на протяжении учебной четверти, полугодия).

Метод группового исследования

Особенность данного метода заключается в том, что группы, сформированные по неформальным признакам, исследуют какой-либо вопрос учебной темы с целью подготовки группового доклада и выступления перед всем классом. Вопросы по теме распределяются между командами так, чтобы в итоге выступлений охватить весь учебный материал новой темы. Внутри команды каждый учащийся исследует свою часть, собирая необходимый материал, предоставляет его в группу, и далее на основе собранных частей формируется общий доклад группы. За подготовленный доклад и выступление каждая команда получает групповую оценку.

Метод «кооп-кооп»

Этот метод очень близок по содержанию к методу группового исследования, но с одним лишь отличием: каждый член группы не просто сдает материал по своей части в команду, но и выступает перед ней с мини-докладом. После того, как сформирован окончательный доклад команды, спикер группы сначала выступает с ним перед командой, и только потом (с учетом изменений и корректив, внесенных членами группы и учителем) – перед всем классом. Дополнительно к этому учащиеся выполняют индивидуальную самостоятельную работу по всей теме. Итоговая оценка группы включает как общий балл за доклад, так и индивидуальные баллы за самостоятельную работу.

Лабораторный метод

Если в классе, например, 32 человека, то учащиеся рассчитываются с 1-го по 8-й, а затем формируют малые группы из «первых», «вторых», «восьмых». Цель учителя заключается в том, чтобы в укомплектованных по случайному признаку группах создать доброжелательную и плодотворную учебную атмосферу. Именно поэтому начало работы в таких группах рекомендуется организовывать с выявления общих интересов, с поиска общей цели, с формирования командного духа, и т.д.

Поисковый метод

Специфика данного метода заключается в формировании поисковых групп учащихся для решения какой-либо практически направленной учебной задачи или выполнения прикладного проекта. Реализация данного метода требует постановки заданий высокого уровня проблемности и предоставления малым группам полной самостоятельности в поисковой деятельности. Именно поэтому разрешается формирование групп по произвольному (зачастую неформальному) признаку, цель которых – провести мини-исследование, требующее творческого, изобретательского подхода, провести статистическую обработку результатов исследования, сформулировать новизну полученных результатов, оформить исследование в виде доклада, и, наконец, пройти «процедуру защиты» основных положений и результатов исследования.

Рассмотренные выше методы далеко не исчерпывают всего арсенала группового обучения. Это лишь наиболее популярные из них. Однако в целом они дают представление о процессуальных характеристиках такого обучения. Естественно, что их можно комбинировать и использовать в сочетании с традиционными методами. Более того, групповая  форма обучения – открытая и динамичная дидактическая система, она постоянно обогащается новыми находками учителей-практиков.

Приложение

Фрагменты урока «Решение тригонометрических уравнений».

Для проведения урока класс делится на три группы, отличающиеся по степени подготовленности учащихся. Все задания дифференцированы в зависимости от уровня группы (наиболее сложные задачи предлагаются III группе).

Задание 1. «Математическое лото».

Группам предлагается набор карточек с тригонометрическими уравнениями и значениями аргумента. Следует собрать лото по принципу домино, начиная с выделенной карточки.

Поощрительные очки получает группа, которая быстрее других правильно соберет лото.
Задания для 1 и 3 групп.

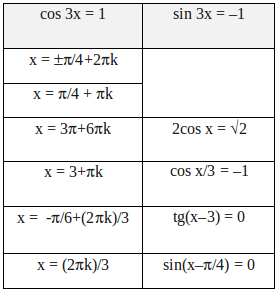
Задание 3. Учащимся каждой из групп предложены карточки с тремя группами заданий. На данном этапе следует внутри группы разработать способы решения двух первых уравнений и осуществить их представителями групп. По два участника групп, которые решали предложенные уравнения на доске, объясняют ход решения каждого. После выступления ребят подводится итог: при  решении тригонометрических уравнений следует выполнить, если это возможно,  разложение на множители.

Далее ученикам предлагается решить первое уравнение из своей индивидуальной карточки путем разложения на множители.

Примеры индивидуальных карточек для участников 2 и 3 групп.

2 группа                                                          3 вариант
Решите уравнения:
1. sin 2x + 2cos x = 1 + sin x
2. 2sin2x – 5cos x + 1 = 0
3. 9sin x – 10cos x = 0
4. 4sin2x + sin x×cos x – 3cos2x = 0

3 группа                                                          4 вариант
Решите уравнения:
1. sin3x×cos x – cos3х×sin x = 0,25
2. cos 4x + 3cos 2x = 1
3. 24sin x – 9cos x = 0
4. 3sin2х + 5sin x×cos x + 4cos2x = 1

Об авторах:

• Кайсина Наталья Александровна, методист НМЦ Выборгского района Санкт-Петербурга,
• Рогачева Татьяна Викторовна, учитель математики ГОУ №103 Санкт-Петербурга.