|
Движение по окружности
|
|
|
miflin | Дата: Вторник, 08.03.2016, 21:30 | Сообщение # 16 |
miflin
Ранг: Профессор (?)
Хмырь обыкновенный
Группа: Пользователи
|
| Сообщений: |
2663 |
| Награды: |
87 |
| Статус: |
Offline |
|
Нема чего сказать в связи с отсутствием точек соприкосновения.
08.03.2016
|
|
|
|
| |
|
|
Casual | Дата: Среда, 09.03.2016, 19:04 | Сообщение # 17 |
Casual
Ранг: Доцент (?)
Группа: Пользователи
|
| Сообщений: |
1323 |
| Награды: |
10 |
| Статус: |
Offline |
|
EricRed, по техническим причинам Александр Игрицкий не может ответить Вам в этой теме.
Он ответил в теме ФИЗМАТ БОЛТОЛОГИЯ.
(дублировать сообщение не буду, дабы не нарушать правил форума)
09.03.2016
Сообщение отредактировал Casual - Среда, 09.03.2016, 19:04
|
|
|
|
| |
|
|
EricRed | Дата: Суббота, 12.03.2016, 20:10 | Сообщение # 18 |
EricRed
Ранг: Студент (?)
Группа: Пользователи
|
| Сообщений: |
170 |
| Награды: |
0 |
| Статус: |
Offline |
|
Цитата Casual (  ) EricRed, по техническим причинам Александр Игрицкий не может ответить Вам в этой теме.
Он только спросил, что значит найти скорость, как я понял. Найти здесь означает сделать неизвестное известным. Необходимо получить значение мгновенной скорости и, разумеется, её погрешность. Это будет результатом её косвенного измерения.
Меня тут ещё всё о каком-то предельном переходе спрашивали. Вот определение предела:
Число A служит пределом величины a, зависящей от t, при t стремящимся к T, если для любого t, бесконечно близкого к T, значение a будет бесконечно близко к A. Если же означенное выполняется не для всех t, бесконечно близких к T, а лишь для некоторых, то предел частичный.
На счёт скорости, по уму бы надо всё нарисовать, всё подробно объяснить, как её тут найти-то. Ведь, я уверен, ужасающе подавляющее большинство присутствующих из результатов измерений найти мгновенную скорость, а тем паче её погрешность, не сумеют.
Меня при том вот что сильно удивляет. Вы представьте себе, что в школе вам рассказали арифметические действия, алгебру, квадратные уравнения. Но после этого вы трёхзначные числа умножать не умеете ни столбиком, ни на калькуляторе. Представили?… Что бы вы сказали о таком вот обучении?… Ведь, сказали бы, не стали бы молчать, правда?… А почему ж вы молчите, когда после курса физики вы не абы что, а даже скорость не в состоянии найти в простейшей задаче? А?
Задача, собственно, так звучит: школьник решил измерять начальную скорость по высоте подъёма и хочет выяснить, существенно ли тут сопротивление воздуха. Для этого он решил исследовать, как тут меняется мгновенная скорость. Он явно хочет не просто установить факт, существенно трение или нет, а исследовать его влияние даже, если оно окажется существенным.
Но, народ, мне лень. Много картинок рисовать и очень много слов писать нужно.
12.03.2016
|
|
|
|
| |
|
|
Casual | Дата: Воскресенье, 13.03.2016, 16:36 | Сообщение # 19 |
Casual
Ранг: Доцент (?)
Группа: Пользователи
|
| Сообщений: |
1323 |
| Награды: |
10 |
| Статус: |
Offline |
|
Цитата EricRed (  ) А почему ж вы молчите, когда после курса физики вы не абы что, а даже скорость не в состоянии найти в простейшей задаче? А?
Почему не в состоянии?
1. Делаем два снимка движущегося тела: снимок А и снимок В спустя dt секунд.
2. Выбираем систему координат и находим положения тела на снимках А и В: р0 и р1.
Например, поместим начало системы координат в положение тела на снимке А. Тогда р0 = (0, 0)
3. Вектор (p1 - p0)/length(p1 - p0) - направление вектора мгновенной скорости тела в точке р0, т.е. на снимке А.
length(p1 - p0) / dt - величина скорости в этой точке.
Чем меньше выберем dt, т.е. чем быстрее сделаем снимки, тем точнее будут наши измерения.
13.03.2016
Сообщение отредактировал Casual - Воскресенье, 13.03.2016, 16:38
|
|
|
|
| |
|
|
miflin | Дата: Воскресенье, 13.03.2016, 17:35 | Сообщение # 20 |
miflin
Ранг: Профессор (?)
Хмырь обыкновенный
Группа: Пользователи
|
| Сообщений: |
2663 |
| Награды: |
87 |
| Статус: |
Offline |
|
Цитата Casual (  ) Чем меньше выберем dt, т.е. чем быстрее сделаем снимки, тем точнее будут наши измерения.
Не, не, не. И ещё раз не. Неужели доводы с миллиметровкой Вас ничему не научили?
Здесь имеем ту же проблему - либо зернистость пленки, либо конечный размер пикселя на матрице.
Т.е. рано или поздно начнется "бешеная пляска", и предел в принципе недостижим.
Были бы во времена Ньютона эти штучки - фиг бы он создал матанализ.
13.03.2016
|
|
|
|
| |
|
|
EricRed | Дата: Пятница, 03.02.2017, 22:23 | Сообщение # 21 |
EricRed
Ранг: Студент (?)
Группа: Пользователи
|
| Сообщений: |
170 |
| Награды: |
0 |
| Статус: |
Offline |
|
Цитата miflin (  ) Были бы во времена Ньютона эти штучки - фиг бы он создал матанализ.
Наоборот. Это всё было известно ещё в ранней античности: самое раннее известное нам имя -- Евдокс (за долго до Архимеда). Так как греки понасобирали то, что до нас от них дошло, со всего мира, то не мудрено, если это всё могло быть понято и ещё раньше, вплодь до шумеров времён изобретения колеса. Сердце кровью обливается поэтому, когда видишь, что вместо матанализа нам осознанно и намеренно преподают какую-то адовую хрень.

03.02.2017
|
|
|
|
| |
|
|
EricRed | Дата: Суббота, 04.02.2017, 00:33 | Сообщение # 22 |
EricRed
Ранг: Студент (?)
Группа: Пользователи
|
| Сообщений: |
170 |
| Награды: |
0 |
| Статус: |
Offline |
|
Так как miflin уже не менее трёх раз по разным поводам эмоционально окрашено упомянул тему миллиметровки, я счёл себя обязанным доделать то, что поленился доделать: найти мгновенную скорость в простейшей задаче.
Итак, школьник что-то запулил, снял зависимость координат от времени и теперь хочет найти мгновенную скорость. Файл данных (data-discr.d) я прицепил. Он, между прочим, содержит весьма поучительные приколы в начале и конце кривой. Время по оси абсцисс в секундах (точность секундомера в 0,1с). Переместилось это нечто за 10 секунд на 100 единиц длины. Вот уж решайте сами, как велико деление шкалы по оси ординат: зависит от того, что и куда двигалось. Мне это -- не суть.
На графике, вроде бы, парабола постоянного отрицательного ускорения. Но, разумеется, не она:
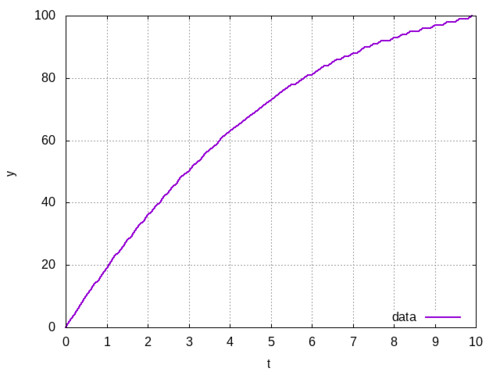
Даже тут глазу видны изломы на которых скорость, понятно, будет бешено скакать.
Первое, что приходит на ум, -- взять более точный секундомер и более точную линейку. Но то ничего не даст: пороговая точность у нас здесь 0,1с и одна единица длины. При более точном измерении будет просто вот что (та же кривая около 2-й секунды движения):
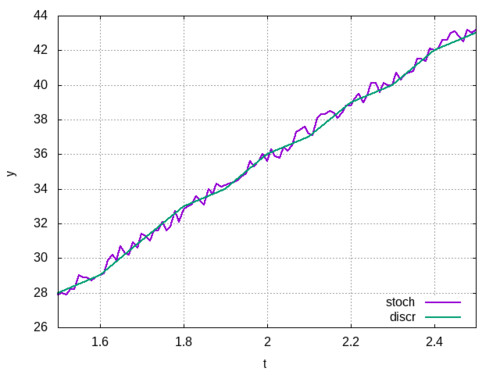
Более точные измерения дают больше точек, но данные зашумлены случайной погрешностью. Повышение точности секундомера и линейки не повышает точности измерения координат и времени, а скорось скачет только ещё безумнее. Пороговая точность нами уже достигнута, ещё точнее мы тут ничего не измерим.
Важно осознать, что даже, если начать скрупулёзно учитывать все посторонние влияния, это мало что даст. Например, если мы измеряем длину карандаша, то, например, тепловые флуктуации мы уж никак не учтём и не исключим: если заморозить карандаш, он растрескается. Поэтому существует пороговая точность, которую мы вообще не в состоянии улучшить.
Откроем теперь учебник Мякишева и применим на практике то, чему нас научил товаришьчьичь Сотский: попробуем найти предел средней скорости. Просто строим её график и смотрим:
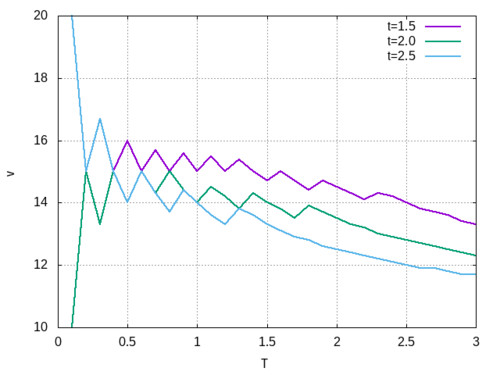
Здесь T -- это интервал времени, на котором вычисляется средняя скорость v как соответствующее отношение для трёх моментов времени около 2-й секунды движения.
Учебник вводит нас в заблуждение: никакого предела при уменьшении T тут и впомине нет. Наоборот: чем меньше интервал, тем безумнее скачет скорость.
Как тогда найти скорость, я школьнику уже подсказал выше: нужно сообразить, с какой примерно величины T средняя скорость начинает эти свои пляски. Здесь это что-то между 0.5 и 1.0 секунды. Это значение и нужно взять в качестве dt -- бесконечно малого времени. Мгновенная скорость тогда будет просто равна dy/dt Но нужно не забыть и про её погрешность. То есть, что тут будет выступать в качестве dv ?
Если время изменится на половину dt то, как за это время изменится скорость? Никак: изменение времени бесконечно мало -- скорость не успеет измениться на конечную величину (в противном случае тело испытывает то, что называется ударом). Поэтому на картинке видна и погрешность: примерно 1 единица длины в секунду. Измерение мгновенной скорости для t=2 дало 15+/-1 единиц длины в секунду.
Заметьте. Секундомер у нас призамечательнейший -- 0.1 секунды отмеряет. А бесконечно малое время -- аж в целую секунду. То есть, всё, где скорость заметно меняется быстрее, чем за секунду, мы измерить вообще не сможем (пороговая точность уже, как говорилось, нами достигнута тут).
Заметьте так же, что семиклассник понял, что такое удар: это, когда скорость меняется на конечную величину (то есть, -- на порядок больше, чем dv) за бесконечно малое время (то есть, -- за время, меньшее dt). Теперь он и профессор могут обсуждать обобщённые функции на одном языке: что такое обобщённые функции семиклассник, конечно, ещё не знает, но основы он понял в совершенно математически строгом виде и может обсуждать их с профессором, говоря с ним на совершенно одном языке. Мы семикласснику это изложили сразу совершенно строго без каких-либо упрощений.
04.02.2017
|
|
|
|
| |
|
|
iyugov | Дата: Суббота, 04.02.2017, 06:42 | Сообщение # 23 |
iyugov
Ранг: Доцент (?)
Группа: Активисты
Должность: Инженер, учитель
|
| Сообщений: |
1191 |
| Награды: |
12 |
| Статус: |
Offline |
|
Первое, что приходит на ум, - не взять ещё линейку, а произвести сглаживание и аппроксимацию настоящей параболой.
Цитата EricRed (  ) попробуем найти предел средней скорости
В какой точке предел?
04.02.2017
|
|
|
|
| |
|
|
EricRed | Дата: Суббота, 04.02.2017, 22:42 | Сообщение # 24 |
EricRed
Ранг: Студент (?)
Группа: Пользователи
|
| Сообщений: |
170 |
| Награды: |
0 |
| Статус: |
Offline |
|
Цитата iyugov (  ) Первое, что приходит на ум, - не взять ещё линейку, а произвести сглаживание и аппроксимацию настоящей параболой.
Тут нет никакой параболы, потому что рядом пролетала ворона и взмахом крыла к чертям сдула всю параболу. О зависимости координаты от времени мы ничего не знаем: мы её и ищем -- смотрим, насколько нелинейно меняется мгновенная скорость. Если сглаживаешь данные скользящим средним, то обязан уметь оценить погрешность, которую оно вносит в результат. А мы это умеем? Имеет смысл сглаживать график средней скорости на разных интервалах (третья картинка): тогда проще взять значение средней скорости, соответствующее dt Но шкурка выделки не стоит: в таких случаях нужно округлять результат так, чтобы скачки вообще не сказывались -- 15+/-1 -- и тогда не важно, в какой именно точке мы взяли среднюю скорость около T=1.0
Цитата iyugov (  ) В какой точке предел?
В любой. На картинке, как сказано, приведены три значения времени: 2.0, 1.5, 2.5 и нарисован график средней скорости при разных интервалах усреднения T.
04.02.2017
|
|
|
|
| |
|
|
iyugov | Дата: Суббота, 04.02.2017, 23:40 | Сообщение # 25 |
iyugov
Ранг: Доцент (?)
Группа: Активисты
Должность: Инженер, учитель
|
| Сообщений: |
1191 |
| Награды: |
12 |
| Статус: |
Offline |
|
EricRed, не параболой, так полиномом. Аппроксимация и проверка адекватности модели. Без этого поиск сколько-нибудь адекватной мгновенной скорости - это пляски с бубном.
А вообще похоже на экспоненту - переходный процесс 1-го порядка. На глаз - 118*(1 - exp(-0,19*t)). Дифференцируется элементарно. Не седьмой класс, но по уму вроде так.
Интересное у вас определение предела.
04.02.2017
Сообщение отредактировал iyugov - Суббота, 04.02.2017, 23:40
|
|
|
|
| |
|
|
EricRed | Дата: Воскресенье, 05.02.2017, 12:04 | Сообщение # 26 |
EricRed
Ранг: Студент (?)
Группа: Пользователи
|
| Сообщений: |
170 |
| Награды: |
0 |
| Статус: |
Offline |
|
Цитата iyugov (  ) EricRed, не параболой, так полиномом.
Не полиномом, так рациональными функциями, не ими, так радом Фурье, не им так, сплайнами, не ими так вейвлетами, не ими так...
Цитата iyugov (  ) Аппроксимация и проверка адекватности модели. Без этого поиск сколько-нибудь адекватной мгновенной скорости - это пляски с бубном.
Модель-то откуда нам взять? Модель выводится из законов физики: учитываем все силы, действующие на тело, получаем закон его движения, подгоняем к данным -- находим значения параметров модели. Но здесь мы и исследуем эти законы физики: мы даже ещё не знаем пока, подчиняется ли движение запуленного тела законам механики. А бывают и случаи в жизни, когда модели в виде простой функции вообще нет и быть не может; но скорости на то начхать -- она как была скоростью так ею и останется.
Цитата iyugov (  ) А вообще похоже на экспоненту
Нет, это полином.
Цитата iyugov (  ) Интересное у вас определение предела.
Оно у меня, но не моё по авторству -- разве что, мог переврать, но, вроде, правильно.
Хотелось бы, чтобы было замечено главное: это определение предела применимо как есть в данной конкретной задаче, потому что dt есть здесь бесконечно малое в самом наипрямом смысле слова. Семиклассник понял, что такое предел функции: это, если для всех t, близких к t0 меньше, чем на dt, будет x близко к x0 ближе, чем на dx.
05.02.2017
|
|
|
|
| |
|
|
iyugov | Дата: Воскресенье, 05.02.2017, 12:25 | Сообщение # 27 |
iyugov
Ранг: Доцент (?)
Группа: Активисты
Должность: Инженер, учитель
|
| Сообщений: |
1191 |
| Награды: |
12 |
| Статус: |
Offline |
|
EricRed, если мало что знаем об объекте, а работать с ним надо, то пробуем разные модели. Физические законы сами выводились экспериментально, разве нет?
Не уловил идею обсуждения: один конкретный семиклассник понял про бесконечно малые, или же это доступно многим его сверстникам?
05.02.2017
|
|
|
|
| |
|
|
EricRed | Дата: Воскресенье, 05.02.2017, 23:51 | Сообщение # 28 |
EricRed
Ранг: Студент (?)
Группа: Пользователи
|
| Сообщений: |
170 |
| Награды: |
0 |
| Статус: |
Offline |
|
Цитата iyugov (  ) EricRed, если мало что знаем об объекте, а работать с ним надо, то пробуем разные модели. Физические законы сами выводились экспериментально, разве нет?
Так что первым-то делается: законы экспериментально устанавливаются или модели пробуются? Здесь школьнику рассказали, что такое координаты и время, научили их измерять (даже погрешности измерений научили оценивать); теперь объясняют, что такое мгновенная скорость, но измерять её учебник не научил, а определение в нём, как показано выше, -- в корне неверное. Причём тут модели? До них ещё пыхтеть и пыхтеть. Тут и законов-то ещё нет: только базовые величины начали вводиться.
Цитата iyugov (  ) Не уловил идею обсуждения: один конкретный семиклассник понял про бесконечно малые, или же это доступно многим его сверстникам?
Я не вижу тут ничего такого, чтобы не было доступно среднестатистическому семикласснику. Доступно следующее: понятия предела последовательности и функции, производной, умение дифференцировать полиномы. И даже с обобщёнными функциями, как я говорил, семиклассник фактически может иметь дело без каких-либо упрощений и нестрогостей. Другое дело, что методика преподавания этого всего для столь раннего возраста может быть сильно сложна, но я не думаю, что для современной педагогики это непосильный труд.
05.02.2017
|
|
|
|
| |
|
|
iyugov | Дата: Воскресенье, 05.02.2017, 23:56 | Сообщение # 29 |
iyugov
Ранг: Доцент (?)
Группа: Активисты
Должность: Инженер, учитель
|
| Сообщений: |
1191 |
| Награды: |
12 |
| Статус: |
Offline |
|
Цитата EricRed (  ) Так что первым-то делается: законы экспериментально устанавливаются или модели пробуются?
Примерно как яйцо и курица.
Есть ли статистически значимый опыт преподавания всего этого матана в среднем звене?
05.02.2017
|
|
|
|
| |
|
|
miflin | Дата: Понедельник, 06.02.2017, 16:53 | Сообщение # 30 |
miflin
Ранг: Профессор (?)
Хмырь обыкновенный
Группа: Пользователи
|
| Сообщений: |
2663 |
| Награды: |
87 |
| Статус: |
Offline |
|
Цитата iyugov (  ) Есть ли статистически значимый опыт преподавания всего этого матана в среднем звене?
В отдельно взятой голове. 
06.02.2017
|
|
|
|
| |
|







