Муниципальное общеобразовательное учреждение

средняя общеобразовательная школа №5.

Урок геометрии в 11 классе

По теме : «Правильные многогранники».

Автор: Морина Светлана Алексеевна

Г.Железноводск.

Урок по теме: «Правильные многогранники».

Тип урока: изучение нового материала.

Цель урока:

Ввести определения правильного многогранника. Рассмотреть свойства правильных многогранников. Познакомить учащихся с историей возникновения и развития теории многогранников.

Задачи:

-Формирование пространственных представлений учащихся.

-Развитие практических навыков учащихся по изготовлению правильных, равноугольно полуправильных, звездчатых многогранников.

-Ознакомление учащихся с правильными многогранниками, их характеристиками;

-Развитие умения наблюдать, умения рассуждать по аналогии, интереса к предмету через использование информационных технологий;

-Воспитание  общетрудовых умений, графической культуры.

Ход урока.

1.Орг.момент.

2. Целеполагание.

Учитель: Есть в школьной геометрии особые темы, которые ждешь с нетерпением, предвкушая встречу с невероятно красивым материалом. К таким темам можно отнести тему "Правильные многогранники". Здесь не только открывается удивительный мир геометрических тел, обладающих неповторимыми свойствами, но и интересные научные гипотезы. Ни одни геометрические тела не обладают таким совершенством и красотой, как правильные многогранники. Сегодня на уроке мы узнаем и увидим много интересного, нам предстоит ответить на такие вопросы, как, например: Какие многогранники называются правильными? Сколько их существует? Что такое Эйлерова характеристика? Какие тела носят название тел Кеплера- Пуансо? И многие- многие другие… И, наконец: где, зачем и для чего нам нужны многогранники? Может быть, в жизни можно обойтись и без них?

3. Изучение нового материала.

Учитель: Мне хотелось бы начать со слов Бертрана Рассела: “Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства”. Название “правильные” идет от античных времен, когда стремились найти гармонию, правильность, совершенство в природе и человеке. Правильные многоугольники – это многоугольники, у которых все стороны и все углы равны, правильные многогранники – это многогранники, ограниченные правильными и одинаковыми многоугольниками.

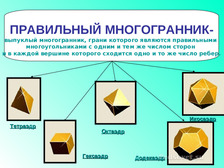
ПРАВИЛЬНЫЙ МНОГОГРАННИК- выпуклый многогранник, грани которого являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине которого сходится одно и то же число ребер.

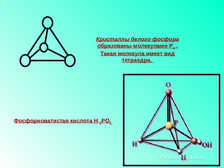
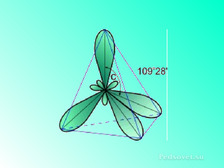
ТЕТРАЭДР – правильный многогранник, поверхность которого состоит из четырех правильных треугольников.

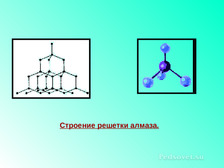
ГЕКСАЭДР (КУБ) – правильный многогранник, поверхность которого состоит из шести правильных четырехугольников (квадратов

ОКТАЭДР – правильный многогранник, поверхность которого состоит из восьми правильных треугольников.

ДОДЕКАЭДР – правильный многогранник, поверхность которого состоит из двенадцати правильных пятиугольников.

ИКОСАЭДР – правильный многогранник, поверхность которого состоит из двадцати правильных треугольников. Названия этих многогранников пришли из Древней Греции, и в них указывается число граней:

«эдра» - грань

«тетра» - 4

«гекса» - 6

«окта» - 8

«икоса» - 20

«додека» - 12

- Все правильные многогранники были известны еще в Древней Греции, и им посвящена заключительная, 13-я книга знаменитых “Начал” Евклида. Как говорилось раньше, эти многогранники часто называют также платоновыми телами – в идеалистической картине мира, данной великим древнегреческим мыслителем Платоном, четыре из них олицетворяли 4 стихии: тетраэдр – огонь, куб – землю, икосаэдр – воду, октаэдр – воздух, пятый же многогранник, додекаэдр, символизировал все мироздание – его по-латыни стали называть quinta essentia (квинта эссенция), означающее все самое главное, основное, истинную сущность чего-либо.

Правильные многогранники в философской картине мира Платона»

Правильные многогранники иногда называют Платоновыми телами, поскольку они занимают видное место в философской картине мира, разработанной великим мыслителем Древней Греции Платоном (ок. 428 – ок. 348 до н.э.).

Платон считал, что мир строится из четырёх «стихий» - огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников. Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у разгоревшегося пламени; икосаэдр – как самый обтекаемый – воду; куб – самая устойчивая из фигур – землю, а октаэдр – воздух. В наше время эту систему можно сравнить с четырьмя состояниями вещества - твёрдым, жидким, газообразным и пламенным. Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим.

Это была одна из первых попыток ввести в науку идею систематизации.

А теперь от Древней Греции перейдём к Европе XVI – XVII вв., когда жил и творил замечательный немецкий астроном, математик Иоганн Кеплер (1571 – 1630).

«Кубок Кеплера»  

П
редставим себя на месте Кеплера. Перед ним различные таблицы – столбики цифр. Это результаты наблюдений движения планет Солнечной системы – как его собственных, так и великих предшественников – астрономов. В этом мире вычислительной работы он хочет найти некоторые закономерности. Иоганн Кеплер, для которого правильные многогранники были любимым предметом изучения, предположил, что существует связь между пятью правильными многогранниками и шестью открытыми к тому времени планетами Солнечной системы. Согласно этому предположению, в сферу орбиты Сатурна можно вписать куб, в который вписывается сфера орбиты Юпитера.

В неё, в свою очередь, вписывается тетраэдр, описанный около сферы орбиты Марса. В сферу орбиты Марса вписывается додекаэдр, в который вписывается сфера орбиты Земли. А она описана около икосаэдра, в который вписана сфера орбиты Венеры. Сфера этой планеты описана около октаэдра, в который вписывается сфера Меркурия. Такая модель Солнечной системы (рис. 6) получила название «Космического кубка» Кеплера. Результаты своих вычислений учёный опубликовал в книге «Тайна мироздания». Он считал, что тайна Вселенной раскрыта. Год за годом учёный уточнял свои наблюдения, перепроверял данные коллег, но, наконец, нашёл в себе силы отказаться от заманчивой гипотезы. Однако её следы просматриваются в третьем законе Кеплера, где говориться о кубах средних растояний от Солнца. Сегодня можно с уверенностью утверждать, что расстояния между планетами и их число никак не связаны с многогранниками. Конечно, структура Солнечной системы не является случайной, но истинные причины, по которым она устроена так, а не иначе, до сих пор не известны. Идеи Кеплера оказались ошибочными, но без гипотез, иногда самых неожиданных, казалось бы, бредовых, не может существовать наука.

«Икосаэдро-додекаэдровая структура Земли»

Идеи Платона и Кеплера о связи правильных многогранников с гармоничным устройством мира и в наше время нашли своё продолжение в интересной научной гипотезе, которую в начале 80-х гг. высказали московские инженеры В. Макаров и В. Морозов. Они считают, что ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов, идущих на планете. Лучи этого кристалла, а точнее, его силовое поле, обуславливают икосаэдро-додекаэдровую структуру Земли (рис.7). Она проявляется в том, что в земной коре как бы проступают проекции вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра.

Многие залежи полезных ископаемых тянутся вдоль икосаэдро-додекаэдровой сетки; 62 вершины и середины рёбер многогранников, называемых авторами узлами, обладают рядом специфических свойств, позволяющих объяснить некоторые непонятные явления. Здесь располагаются очаги древнейших культур и цивилизаций: Перу, Северная Монголия, Гаити, Обская культура и другие. В этих точках наблюдаются максимумы и минимумы атмосферного давления, гигантские завихрения Мирового океана. В этих узлах находятся озеро Лох-Несс, Бермудский треугольник. Дальнейшие исследования Земли, возможно, определят отношение к этой научной гипотезе, в которой, как видно, правильные многогранники занимают важное место.

А сейчас от научных гипотез перейдём к научным фактам.

4. Практическая работа .

Работа в группах.(группы формируются дифференцированно, более подготовленной группе предлагается более сложное задание.)

1 группа- доказать, что правильных многогранников 5.

2 группа- вывести формулы полной поверхности правильных многогранников.

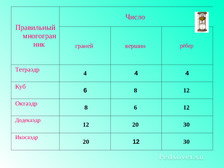
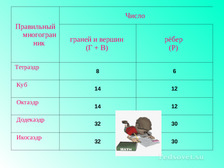
3 группа- заполнить таблицы и сделать вывод.(использовать модели).

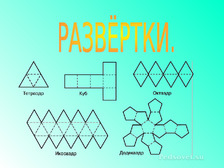
4 группа- нарисовать развертки правильных многогранников (на компьютере).

5. Отчет групп о работе.

Один представитель группы отчитывается о результатах .

Учащиеся делают соответствующие записи в тетради.

- формулы площадей;

- теорему Эйлера.

6. Дополнительные сведения.

Учитель: Кроме пяти правильных многогранников существуют полуправильные многогранники, тела Архимеда.

Архимедовы тела обладают свойством: любые две вершины можно совместить так, что все грани многогранника попарно совпадут друг с другом.

Кроме полуправильных многогранников, из правильных многогранников – Платоновых тел можно получить так называемые правильные звездчатые многогранники. Их всего четыре. Первые два были открыты И. Кеплером (1571 – 1630 гг.), а два других были построены почти двести лет спустя французским математиком и механиком Луи Пуансо (1777 – 1859 гг.). Именно поэтому правильные звездчатые многогранники получили название тел Кеплера – Пуансо. В работе «О многоугольниках и многогранниках» (1810 г.) Луи Пуансо перечислил и описал все правильные звездчатые многогранники, поставил, но не решил вопрос о существовании правильных многогранников, число граней которых отлично от 4, 6, 8, 12, 20.Отчет на этот вопрос был дан год спустя, в 1811 году, французским математиком Огюстом Луи Коши (1789 – 1857 гг.) в работе «Исследование о многогранниках». В ней доказывается, что не существует других правильных многогранников, кроме перечисленных Пуансо. Автор приходит к выводу, что правильные звездчатые многогранники получаются из выпуклых правильных многогранников путем продолжения их ребер или граней, исследуется вопрос, из каких именно правильных многогранников могут быть получены правильные звездчатые многогранники. Делается вывод о том, что тетраэдр, куб и октаэдр не имеют звездчатых форм, додекаэдр имеет три, а икосаэдр – одну звездчатую форму (это малый звездчатый додекаэдр, большой додекаэдр и большой икосаэдр).

Луи Кэрролл писал: "Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук".

В глубины каких наук пробрались правильные многогранники? Где в жизни мы можем их повстречать?

7. Доклады учащихся.(сопровождаются компьютерными презентациями).

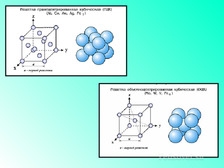
-Правильные многогранники и химия.

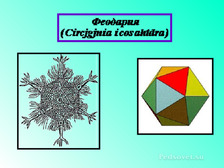
-Правильные многогранники в биологии.

8. Подведение итогов. Выставление оценок.

При наличии времени можно провести тест первичного закрепления.

9. Домашнее задание.

-Изготовить модели правильных многогранников.

-Подготовить реферат о связи правильных многогранниках с различными областями деятельности человека.

10 Рефлексия.

-Что понравилось на уроке?

-Какой материал был наиболее интересен?

-В каких еще областях деятельности можно встретиться с правильными многогранниками?