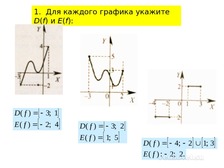
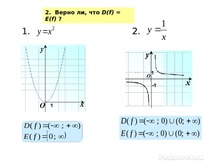
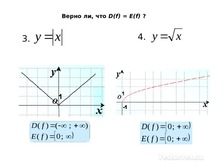
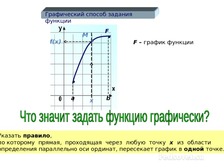
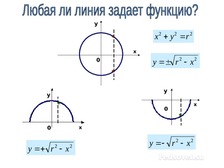
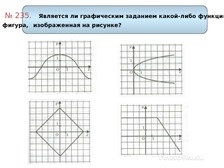
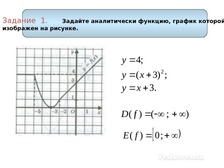
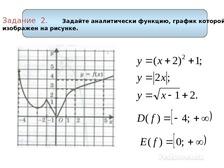
Урок + презентация по алгебре по теме: «СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ» для 9 кл.

Слайд 1

ТЕМА УРОКА

Слайд 2

1. Для каждого графика укажите D(f) и E(f): D( f )   3; 1 E ( f )   2; 4 D( f )   3; 2 E ( f )  1; 5 D( f )   4;  2  1; 3 E ( f ) :  2; 2.

Слайд 3

2. Верно ли, что D(f) = E(f) ? 1. у х 2 D ( f ) ( ;  ) E ( f )  0 ;  1 2. у  х D( f ) ( ; 0)  (0;  ) E ( f ) ( ; 0)  (0;  )

Слайд 4

Верно ли, что D(f) = E(f) ? 3. у х D ( f ) ( ;  ) E ( f )  0 ;  4. у х D( f )  0 ;   E ( f )  0 ;  

Слайд 5

2. Укажите область определения функции. х 1 у ( х  2)( х  3) 2 у х  3 х  4 х у х 2 D( f ) : x  2; x 3 D( f ) ( ;  ) D( f )    ; 0   2;  

Слайд 6

Указать правило, которое позволяет произвольно выбранному значению х из D(f) найти соответствующее значение у.

Слайд 7

Аналитический способ задания функции Если правило связано с формулой или несколькими формулами – то такой способ задания функции называется аналитическим. у 2  х 9 нет. у  9  х  x 2 , если х 0, f ( x)   х  3, если х  0. 2 у 2 х  3  x 2 , если х 2, f ( x)   2 x  3, если х  0. да да нет, ( ;  2)  (0 ;  ) (0; 2

Слайд 8

Графический способ задания функции F М f(x) F – график функции a x b Указать правило, по которому прямая, проходящая через любую точку х из области определения параллельно оси ординат, пересекает график в одной точке.

Слайд 9

у x 2  y 2 r 2 x 0 y  r 2  x 2 у у 0 0 у  r 2  x 2 x у  r 2  x 2 x

Слайд 10

№ 235. Является ли графическим заданием какой-либо функции фигура, изображенная на рисунке?

Слайд 11

Задание 1. Задайте аналитически функцию, график которой изображен на рисунке. у 4; 2 у ( х  3) ; у х  3. D( f ) ( ;  ) E ( f )  0 ;  

Слайд 12

Задание 2. Задайте аналитически функцию, график которой изображен на рисунке. 2 у ( х  2)  1; у  2х ; у  х  1  2. D( f )   4;   E ( f )  0;  

Слайд 13

Табличный способ задания функции При этом способе приводится таблица, в которой указаны значения функции для конечного множества значений аргумента. 4096

Слайд 14

Словесный способ задания функции – когда правило задания функции описывается словами. № 1. Функция у = f(x) задана на множестве однозначных натуральных чисел с помощью следующего правила: каждому числу х ставится в соответствие удвоенное его значение. x f(x) 1 7 2 2 4 8 6 3 9 8 16 4 10 18 5 12 6 14

Слайд 15

№2. Функция задана таблицей: х 1 2 3 4 5 6 7 8 9 f(x) 1 4 9 16 25 36 49 64 81 а) Составьте словесное описание этой функции; б) Изобразите функцию графически.

Слайд 16

1. Аналитический 2. Графический 3. 4.Табличный Словесный 1. Знать D(f) . 2. Указать правило, которое позволяет произвольно выбранному значению х из D(f) найти соответствующее значение у.

Слайд 17

Самостоятельная работа Вариант 1. Вариант 2. № 237 № 238 № 221 (а, б) № 221 (в, г) №228 (а) №228 (в) Задание на дом: § 8, № 240, 232, 226(в,г). Творческое задание: придумайте функцию, задаваемую аналитически, графически, таблично и словесной формулировкой. (Функции могут быть разными, а может быть одна

Слайд 18

Вариант 1. № 238 № 237 а ) у  х  2 в) у  х  4 б) у  2х  2 № 237 г ) у  ( х  2) 2  4 а ) да б ) нет № 228 (а) а ) да № 237 б ) нет 2 x 1 x 3 2 x 1 2 x 1 0, f ( x)  x 3 x 3 1 f ( x) 0, если х  , х 3 2 2 х 1 у х 3 № 228 (в)  2 х  1 0, х  1 ,   2 х  3  0 ,   х 3. 1  2 Вариант а2. ) у х 2 3 D( f )  3;   х  y 1 2 3 х 1 D( f ) ( ;     3;   2

Слайд 19

Полный текст материала Урок + презентация по алгебре по теме: «СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ» для 9 кл. смотрите в скачиваемом файле.
На странице приведен фрагмент.

Автор: Мелёшина Вера Владимировна → alkin400

15.06.2009

45242

10738

Комментировать

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.

Вход | Регистрация

запомнить
Забыл пароль \| Регистрация