Главная → Файлы для скачивания → Математика, алгебра, геометрия → К уроку

Презентации по математике для 9 класса на тему: "Уравнения, приводимые к квадратным".


УВАЖАЕМЫЕ РЕБЯТА!

Просим Вас ответить на данные вопро­сы.

    • Ваше отношение к уроку:

      1. Мне понравилось заниматься;

      2. Мне было трудно;

      3. Математика точно не для меня;

      4. Другое ________________________________________________

        • С каким настроением Вы шли на данный урок? (поставьте «галочку» около соответствующего знака)

          • _______

            • _______

              • _______



    • Считаете ли Вы, что цели данного урока достигнуты?

      1. да;

      2. нет.

    • Усвоили ли Вы главное в изученной теме?

      1. да;

      2. нет.

    • Научились ли Вы решать задачи по теме урока?

      1. да;

      2. нет.

        • Поставьте «галочку» около соответствующего знака, который отвечает Вашему настроению по окончании урока:

          • _______

            • _______

              • _______



Спасибо за ответы.

Слайд 1
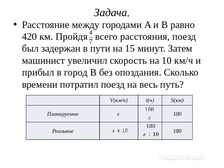
Задача. • Расстояние между городами A и B равно 420 км. Пройдя всего расстояния, поезд был задержан в пути на 15 минут. Затем машинист увеличил скорость на 10 км/ч и прибыл в город B без опоздания. Сколько времени потратил поезд на весь путь? V(км/ч) t(ч) S(км) Планируемое 180 Реальное 180
Слайд 2
Решение - Не удовлетворяет условию задачи Ответ: 5,25 ч
Слайд 1
«ИЗУЧИТЕ АЗЫ НАУКИ, ПРЕЖДЕ ЧЕМ ВЗОЙТИ НА ЕЁ ВЕРШИНЫ. НИКОГДА НЕ БЕРИТЕСЬ ЗА ПОСЛЕДУЮЩЕЕ, НЕ ОСВОИВ ПРЕДЫДУЩЕЕ» И.П. Павлов. 1 2 3 4 5 6 7 8 9 10 11 12
Слайд 2
Вопрос 1  Какое уравнение с одной переменной называется целым?
Слайд 3
ОТВЕТ:  Уравнение, в котором левая и правая части являются целым выражением.
Слайд 4
Вопрос 2  Как найти степень целого уравнения?
Слайд 5
ОТВЕТ:  Если уравнение с одной переменной написано в виде многочлена стандартного вида, то степень этого многочлена называют степенью уравнения.
Слайд 6
Вопрос 3  Сколько корней может иметь квадратное уравнение?
Слайд 7
ОТВЕТ: Число корней квадратного уравнения зависит от дискриминанта.  Если D>0, то уравнение имеет 2 корня.  Если D=0, то уравнение имеет 1 корень.  Если D
Слайд 8
Вопрос 4  Сколько корней может иметь уравнение n-ой степени?
Слайд 9
ОТВЕТ:  Уравнение n-ой степени имеет не более n корней.
Слайд 10
Вопрос 5  Дайте определение биквадратного уравнения.
Слайд 11
ОТВЕТ:  Уравнение вида , где называется биквадратным уравнением.
Слайд 12
Вопрос 6  Сформулируйте определение квадратного уравнения.
Слайд 13
ОТВЕТ:  Квадратным уравнением называется уравнение вида , где xпеременная, a, b, c – некоторые числа, причём
Слайд 14
Вопрос 7  Какое уравнение называют неполным квадратным уравнением?
Слайд 15
ОТВЕТ:  Если в квадратном уравнении хотя бы один из коэффициентов b или c равны нулю. Такое уравнение называют неполным квадратным уравнением.
Слайд 16
Вопрос 8  Что значит решить уравнение?
Слайд 17
ОТВЕТ:  Решить уравнение с одной переменной – значит найти все его корни или доказать что корней нет.
Слайд 18
Вопрос 9  Как читается теорема обратная теореме Виета?
Слайд 19
ОТВЕТ:  Если m и n таковы, что их сумма равна – p, а произведение равно q, то эти числа являются корнями уравнения .
Слайд 20
Вопрос 10  Назовите известные вам способы решения квадратных уравнений.
Слайд 21
ОТВЕТ: Решение квадратных уравнений, путём выделения квадрата двучлена.  Решение квадратных уравнений по формуле. Формула корней квадратного уравнения:  Для квадратных уравнений, у которых второй коэффициент является чётным числом, формулу корней удобно записывать в другом виде:   , Графический способ. Разложением на множители.
Слайд 22
Вопрос 11  Что называют корнем уравнения?
Слайд 23
ОТВЕТ:  Корнем уравнения называется значение переменной, при котором уравнение обращается в верное равенство.
Слайд 24
Вопрос 12  Какое уравнение называется приведённым квадратным уравнением?
Слайд 25
ОТВЕТ:  Квадратное уравнение, в котором первый коэффициент равен 1, называют приведённым квадратным уравнением.
Слайд 1
Определите вид каждого -1;1 Квадратное уравнение уравнения и найдите его корни. -1,6 -1,6 0;5 Корней нет 5;9 -4;-1 Приведённо е квадратное уравнение Неполное квадратное уравнение -6;6 -1;0 -1 -1;6 Линейное уравнение Дробнорациональн ое уравнение
Слайд 1
Замена 5x + 1 = t, По теореме, обратной теореме Виета, Вернёмся к подстановке 5x + 1 = t, получим 5x + 1 = -7 5x + 1 = 1 5x = -8 5x = 0 x = -1,6 x=0 Ответ: -1,6;0
Слайд 2
Тема урока: «Уравнения, приводимые к квадратным»  Цель нашего урока: Научиться решать уравнения, приводимые к квадратным, путём введения вспомогательной переменной. Счет и вычисления - основа порядка в голове. (Песталоцци)
Слайд 3
Замена 5x + 1 = t, По теореме, обратной теореме Виета, Вернёмся к подстановке 5x + 1 = t, получим 5x + 1 = -7 5x + 1 = 1 5x = -8 5x = 0 x = -1,6 x=0 Ответ: -1,6;0
Слайд 4
Данное уравнение Ввод новой переменной Квадратное уравнение Решение Ре ше ни е Корни уравнения Уравнения, определяемые подстановкой Возврат к прежней переменной Корни квадратного уравнения
Слайд 5
ДОМАШНЕЕ ЗАДАНИЕ:   Попытайтесь решить последнее уравнение, А ТАКЖЕ: используя ДРУГИЕ замены: п.10,11. I II №220(в,г) №221(б) №225 ПРОАНАЛИЗИРОВАТЬ И ОТВЕТИТЬ НА ВОПРОСЫ: На оценку «5»в №228 Появилось ли что-нибудь новое процессе замены переменной по сравнению с предыдущей заменой? Какая из всех замен представляется вам наиболее рациональной?
Слайд 6
ЗАКРЕПЛЕНИЕ:
Слайд 7
, тогда Пусть По теореме, обратной теореме Виета: или Ответ:
Слайд 8
, тогда Пусть По теореме, обратной теореме Виета: или Решений нет Ответ:
Слайд 9
, Пусть тогда По теореме, обратной теореме Виета: или Ответ: -4;4 ; ;
Слайд 10
Пусть , тогда По теореме, обратной теореме Виета: или Ответ:
Слайд 1
 Первым формулу для решения кубического ФОРМУЛЫ ДЛЯ РЕШЕНИЯ КУБИЧЕСКИХ УРАВНЕНИЙ  уравнения нашёл профессор Болонского университета Сципион дель Ферро(ок. 1515 г.). Свой способ решения он передал преемнику по кафедре Аннибалу делла Наве. А также своему ученику Антонио Фиоре. Он использовал этот способ для составления задач на кубические уравнения. Учитель математики Жуану де Кои решая эти задачи обратился за помощью к своему другу Николо Тарталье. Тарталья сумел продвинуться в решении этих задач и публично заявил об этом. Фиоре сочтя это заявление похвальбой вызвал Тарталью на поединок и проиграл его.
Слайд 2
Сципион дель Ферро (1465-1526 г.г.)  Сципион был известен как крупный учёный и прекрасный лектор. Есть сведения о том, что его лекции в Болонье слушал Николай Коперник.
Слайд 3
Никколо Тарталья Выходец из бедной (1500-1557 семьи, самоучка. Своё г.г.) прозвище – “tartaglia”(заика) получил за то, что с трудом говорил после раны, полученной в детстве.
Слайд 4
Джироламо Кардано (1501-1576 г.г.) Джироламо Кардано был чрезвычайно ярким и талантливым человеком. Как врач он пользовался широкой известностью, получал лестные приглашения на службу от знатных особ. Периоды творческой активности у него чередовались с бездействием, когда он предавался азартным играм. Именно Кардано, на редкость удачливый игрок, сделал первую попытку создать математическую теорию азартных игр.
Слайд 5
Поединок между Тартальей и Феррари. В 1547 году в Милане состоялся поединок между Тартальей и Феррари, где более искушённый в дискуссиях Феррари, по-видимому, одержал победу.

Полный текст материала Презентации по математике для 9 класса на тему: "Уравнения, приводимые к квадратным". смотрите в скачиваемом файле.
На странице приведен фрагмент.
Автор: Луконенко Лариса Николаевна →  ParaBeLLum
25.10.2009 0 11380 4571

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.

Скачать материал с Pedsovet.su Скачать материал