Главная → Файлы для скачивания → Математика, алгебра, геометрия → К уроку

Урок математики на тему «Определенный интеграл» для 11 класса


Приложение 1




Карточка №1


Вычислите




Карточка №2



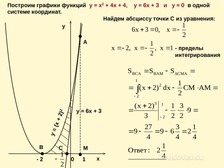
Найти все а, при которых площадь фигуры, ограниченной линиями у = х2 + 4х + 4, х = - 1, х = а, у = 0 равна 5.



Автор: Лушина Татьяна Владимировна

Полное название образовательного учреждения: Муниципальное общеобразовательное учреждение лицей (г.Орехово-Зуево Московской области)

Предмет: алгебра и начала анализа

Класс: 11 класс (физмат)

Тема урока: Обобщающий урок по теме «Определенный интеграл»

Цель урока: обобщение и систематизация знаний по теме

Задачи урока:

образовательные:

  • углубление понимания сущности определенного интеграла путем применения его для получения новых знаний;

  • развитие умений и навыков применять определенный интеграл при решении задач;

воспитательные:

  • воспитание познавательного интереса к учебному предмету;

  • воспитание у учащихся культуры мышления;

  • формирование умений осуществлять самоконтроль;

развивающие:

  • формирование умений строить доказательства, логическую цепочку рассуждений;

  • формирование умений проводить обобщение, переносить знания в новую ситуацию

Учебно-методическое обеспечение: Алгебра и математический анализ для 11 класса: Учеб.пособие для учащихся шк. и классов с углубл. изуч. математики / Н.Я. Виленкин, О.С. Ивашев-Мусатов, С.И. Шварцбурд. – 4-е изд. – М.: Просвещение, 1995.

Время реализации урока: 1 урок (45 минут)

Авторский медиапродукт:

1. редактор Microsoft Power Point, текстовый редактор Microsoft Word.

2. вид мадиапродукта: наглядная презентация учебного материала.

Необходимое оборудование и материалы для урока-занятия: компьютер, мультимедийный проектор, экран, слайды, составленные учителем, карточки.

План проведения урока (занятия):


Этапы урока

Временная реализация

  1. Организационный момент

  • Вступительное слово учителя

2 мин

  1. Проверка домашней работы

5 мин

  1. Работа с классом

  • Фронтальный опрос

  • Самостоятельная работа у доски и на местах с последующей проверкой

23 мин

  1. Презентация творческих заданий

10 мин

  1. Подведение итога урока

4 мин

  1. Задание на дом

1 мин


Ход урока:

I. Организационный момент.


Сегодня заключительный урок по теме: «Определенный интеграл». Предстоит контрольная работа. Перед вами задача – показать как вы усвоили эту тему и умеете ее применять при решении задач.


II. Проверка домашней работы.


На экране мультимедийного проектора показываю слайды 1 – 6.

Учащиеся на экране видят правильное решение и оформление домашних задач. Те, кто допустил ошибки, исправляют их.


III. Работа с классом.


Вопросы.

  1. Что такое определенный интеграл?

  2. Какие значения может принимать определенный интеграл?


К доске вызываются два ученика для работы на крутящихся досках с обратной стороны, которые выполняют задания под диктовку, а все остальные в тетрадях.


Задание.

Вычислить интеграл:


По записям учеников, работающих у доски, учащиеся проверяют свои работы, работы отвечающих и оценивают их.


Критерий выставления оценки:

5 заданий – «5» 3 задания – «3»

4 задания – «4» 2 задания – «2»


Вызываются к доске два ученика, которые выполняют задания по карточке (см. Приложение 1).


Пока учащиеся работают у доски, провожу фронтальный опрос.


Вопросы.


  1. В чем состоит геометрический смысл интеграла?

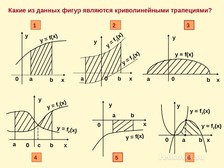
  2. Что такое криволинейная трапеция?



  1. Какие из данных фигур являются криволинейными трапециями?




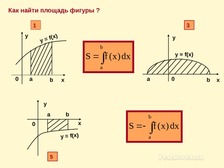
  1. Как найти площадь фигур 1 и 3?

  2. Как найти площади фигуры 5?

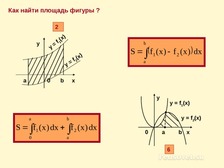
  3. Как найти площади фигуры 2?

  4. Как найти площади фигуры 4?

  5. Как найти площади фигуры 6?

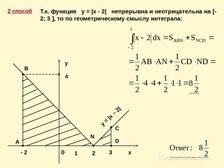
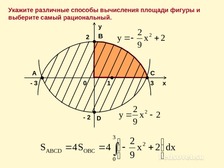
  6. Укажите различные способы вычисления площади фигуры и выберите самый рациональный.


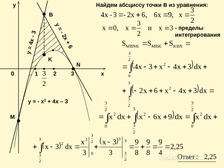
  1. Как найти площадь фигуры, ограниченной графиками функций

у = 3х3 + 7х2 + 6х – 2 и у = 3х3 + 6х2 + 2х – 2


Вопросы 3 – 10 предлагаются учащимся с использованием мультимедийного проектора – слайды 7 – 11.


Отвечающие у доски по своим записям комментируют выполнение заданий по карточкам.



IV. Презентация творческих заданий.


За две недели до открытого урока в домашнюю работу были включены два задания повышенной сложности.

1. Сравнить числа: и 2.


2. На графике функции f(x) = x (2 |x| + x) найдите все точки с отрицательными абсциссами такие, что площадь фигуры, ограниченной касательной к графику, проведенной через каждую из таких точек, и самим графиком равна 36.


Из множества решений, предложенных учащимися, были выбраны самые рациональные, которые и были представлены на открытом уроке с использованием мультимедийного проектора.


V. Подведение итога урока.


Выставление оценок и их комментирование. Дается оценка работы класса.


VI. Задание на дом.


№1045 (б), №1057 (б), №1048 (б)

(Мордкович А.Г. Алгебра и начала анализа. 10-11 кл.)


Список использованной литературы и Интернет-ресурсов:

1. Алгебра и математический анализ для 11 класса: Учеб.пособие для учащихся шк. и классов с углубл. изуч. математики / Н.Я. Виленкин, О.С. Ивашев-Мусатов, С.И. Шварцбурд. – 4-е изд. – М.: Просвещение, 1995.

2. Углубленное изучение курса алгебры и математического анализа: Метод. рекомендации и дидакт. материалы: Пособие для учителя / М.Л. Галицкий, М.М. Мошкович, С.И. Шварцбурд. – 2-е изд., дораб. – М.: Просвещение, 1990.

3. Задачи письменного экзамена по математике за курс средней школы: условия и решения. Вып. 3 / Авт. Л.И. Звавич, Л.Я. Шляпочник. – М.: Школа-Пресс, 1994.

Слайд 1
ОБОБЩАЮЩИЙ УРОК ПО ТЕМЕ: «ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ»
Слайд 2
Домашняя работа №1 Найти ту первообразную функции f(x) = 2x + 4, график которой касается прямой у = 6х + 3. Вычислить площадь фигуры, ограниченной графиком найденной первообразной и прямыми у = 6х + 3, у = 0. Решение F(x) = x2 + 4x + c – общий вид первообразных функции f. Найдем с: 1 способ Т.к. график функции F касается прямой у = 6х + 3, то по геометрическому смыслу производной F ’(x) = k, F ‘(x) = 6, 2x + 4 = 6, x = 1. Если х = 1, то у = 6 + 3 = 9. А (1; 9) – точка касания. Т.к. парабола проходит через т.А, то F(1) = 9 F(1) = 1 + 4 + c = 5 + c, 5 + c = 9, c = 4 2 способ Т.к. парабола и касательная имеют только одну общую точку, то уравнение x2 + 4x + c = 6х + 3 имеет единственный корень (D = 0), тогда x2 – 2x + c – 3 = 0 D1 = 1 – c + 3 = - с + 4, - с + 4 = 0, с = 4 Следовательно, F(x) = x2 + 4x + 4
Слайд 3
Построим графики функций y = x2 + 4x + 4, у = 6х + 3 и y = 0 в одной системе координат. Найдем абсциссу точки С из уравнения: 1 у 6 x  3 0, x  А 2 1 x  2, x  , x 1 - пределы 2 интегрирования SBCA SBAM  SCMA  1 1  ( x  2) dx  CM AM  2 2 2 y= (x + 2) 2 у = 6х + 3 В -2 С 1  2 М 0 1 х ( x  2) 3  3 1 3   9  2 2 2 1 27 3 1 9  9  6 2 4 4 4 1 Ответ : 2 4
Слайд 4
№2 Вычислить площадь фигуры, ограниченной параболой у = - х2 + 4х – 3 и касательными к ней в точках с абсциссами х = 0 и х = 3. Решение Найдем уравнение касательных к графику функции f(x) = - x2 + 4x – 3 в точках х = 0 и х = 3. y = f(x0) + f ‘(x0)(x – x0) – уравнение касательной в общем виде x0 = 0 1) f(0) = - 3 2) f ‘(x) = - 2x + 4 3) f ‘(0) = 4 4) y = - 3 + 4(x – 0) y = 4x – 3 x0 = 3 1) f(3) = - 9 + 12 – 3 = 0 2) f ‘(3) = - 2 3) y = - 2(x – 3) y = - 2x + 6 Построим графики функций одной системе координат: у = - х2 + 4х – 3, y = 4x – 3, y = - 2x + 6 в у = - х2 + 4х – 3 – графиком является парабола. (2; 1) – вершина параболы y 4 x  3 x y 0 1 3 1 y  2 x  6 x y 3 0 2 2
Слайд 5
y Найдем абсциссу точки В из уравнения: 3 4x - 3 - 2x  6, 6x 9, x  2 3 x 0, x  и x 3 - пределы 2 интегрирования SMBNK SMBK  SKBN  B -2 y=4 x-3 y= x+ 6 K 0 3 2 1 3 2 N 2 х 3   4 x  3  x 2  4 x  3 dx  0 3     2x  6  x 2  4x  3 dx  у = - х2 + 4х – 3 3 2 3 2 3 2 3 x 2 dx   x 2  6 x  9  dx x 2 dx  M 3 2 0 3 3 3 2 x 2   x  3 dx  3 3 2 0 3  x  3  3 3 3 2 0 9 9 9    2,25 8 8 4 Ответ : 2,25
Слайд 6
3 №3 Вычислить: x  2 dx 2 Решение 1 способ x 2 На [-2; 2], |x – 2| = - x + 2 На (2; 3], |x – 2| = x - 2  -2 3 2 3 2 2 2  2 3 x x  2 dx    x  2 dx   x  2 dx   x2  2  x2 3    2x     2 x    2  2  2 2 9 9 1  2  4  ( 2  4)   6  (2  4) 2  6   4 8 2 2 2
Слайд 7
2 способ Т.к. функция у = |х - 2| непрерывна и неотрицательна на [2; 3 ], то по геометрическому смыслу интеграла: 3 x  2 dx S ABN  S NCD  2 1 1  AB AN  CD ND  2 2 1 1 1  4 4  1 1 8 2 2 2 y B 4 y = |x C N A -2 0 1 2 – 2| D 3 x 1 Ответ : 8 2
Слайд 8
ОБОБЩАЮЩИЙ УРОК ПО ТЕМЕ: «ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ»
Слайд 9
Какие из данных фигур являются криволинейными трапециями? 1 у 2 (х) f = y y y = 3 x) ( f1 y y= 0 a b y х a 0 (x) f 1 = y b a 0 c 4 b y = f(x) x a 0 y b y a y = f (x) 2 x) ( f2 y = f1(x) b x 0 y = f(x) x 5 x y = f2(x) 0 a b x 6
Слайд 10
Как найти площадь фигуры ? 1 у 3 (х) f = y y b S f ( x ) dx y = f(x) a 0 a b a х 0 y a b b x 0 y = f(x) 5 S  f ( x ) dx a b x
Слайд 11
Как найти площадь фигуры ? 2 y y = x) ( f1 b (x) f2 = y a 0 b S  f1 ( x )  f 2 ( x )  dx a x y a y = f2(x) b S f1 ( x ) dx  f 2 ( x ) dx 0 y = f1(x) a 0 a b x 6
Слайд 12
Укажите различные способы вычисления площади фигуры и выберите самый рациональный. y 2 2 2 y  x  2 9 B A -3 C 0 1 3 2 2 y x  2 9 -2 D 3 SABCD 4 SOBC x  2 2  4   x  2  dx 9  0
Слайд 13
Как найти площадь фигуры, ограниченной графиками функций у = 3х3 + 7х2 + 6х – 2 и у = 3х3 + 6х2 + 2х – 2 Решение 3х3 + 7х2 + 6х – 2 = 3х3 + 6х2 + 2х – 2, х2 + 4х = 0, х(х + 4) = 0 х = 0, х = - 4 0  2  S  x  4 x dx 4
Слайд 14
ОБОБЩАЮЩИЙ УРОК ПО ТЕМЕ: «ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ»
Слайд 15
Домашнее задание № 1045 (б), № 1057 (б), №1048 (б)

Полный текст материала Урок математики на тему «Определенный интеграл» для 11 класса смотрите в скачиваемом файле.
На странице приведен фрагмент.
Автор: Лушина Татьяна Владимировна →  TatyanaL
26.12.2012 0 14321 2878

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.


А вы знали?
Как не реагировать на негатив? Почему меня ранит критика и высказывания других людей
Шесть советов, как запустить сарафанное радио репетиторам и экспертам

Инструкции по ПК
Как оплатить ZOOM из России в 2023 году? Как оплатить и другие зарубежные сервисы, заблокированные из-за «санкций»?
Как работать в Canva в России после 01.06.22. Через какой VPN открыть Canva на компьютере?