Разработка урока + презентация "Первообразная. Площадь фигуры"
Самоанализ урока.
Тема урока: Первообразная. Площадь фигуры.
Это один из последних уроков главы «Производная. Интеграл». Урок соответствует программе. На уроке были поставлены следующие задачи:
образовательные: Повторить и обобщить тему, выявить пробелы, рассмотреть нестандартные задачи.
задачи развития: Развивать и совершенствовать культуру математического труда, математическую речь.
воспитательные: Воспитывать умение объективно и реально оценивать свои знания.
Структура урока была такова.
Ознакомление с целью и задачами урока, инструктаж учащихся по организации работы на уроке.
Проверка знаний учащимися фактического материала и их умений раскрывать элементарные внешние связи в предметах и явлениях.
Проверка знаний учащимися основных понятий, правил, законов и умений объяснить их сущность, аргументировать свои суждения и приводить примеры.
Проверка умений учащихся самостоятельно применять знания в стандартных условиях.
Проверка умений учащихся применять знания в измененных, нестандартных условиях.
Дополнительная задача.
Подведение итогов.
Домашнее задание.
Выбранная структура была рациональна для решения задач урока, т.к. данный урок – это урок проверки и коррекции знаний и умений. Это урок базовой системы, и определяя его структуру я исходила из принципа постепенного нарастания уровня знаний и умений, т.е. от уровня осознания до репродуктивного и конструктивного уровней.
Главный акцент на уроке делался на этапе проверки умений учащихся самостоятельно применять знания в стандартных условиях, т.к. задачи этого этапа входят в ЕГЭ. Задания подобраны таким образом, что выбрано главное, существенное для подготовки к экзаменам.
На уроке осуществлялся дифференцированный подход к учащимся. Как было уже сказано выше задания подбирались по нарастанию сложности.
На уроке использовался мультимедийный проектор. Это повысило наглядность урока.
Высокая работоспособность учащихся в течение урока обеспечивалась за счет готового краткого конспекта урока. Это повысило также эффективность урока.
На уроке поддерживалась хорошая психологическая атмосфера общения. Воспитательное влияние личности учителя было реализовано за счет взаимоуважения учеников и учителя.
План урока был выполнен, цель урока достигнута. К такому выводу пришли сами дети. Предложенное домашнее задание было оптимальным по содержанию, в том числе дифференцированным.
Деятельность учащихся я оцениваю следующим образом: на уроке чётко проявился интерес к предмету, эмоциональное состояние учащихся было приподнятым в начале и к концу урока. На уроке присутствовали самоконтроль и самокоррекция со стороны ребят. Была высока степень самостоятельности в учебной деятельности. Внешний вид и организованность ребят способствовали успешному достижению цели урока.
Урок удался, так как мною созданы условия для максимального влияния образовательного процесса ан развитие индивидуальности ребёнка.
МОУ «Октябрьская СОШ» Ардатовского района Республики Мордовия
Урок проверки и коррекции знаний и умений
по теме
" Первообразная. Площадь фигуры"
Урок подготовила учитель математики и информатики
Михатова Марина Николаевна
|
|
|
||||||||
|
|
Оценочный лист учени(ка)цы 11 класса __________________________________
|
||||||||
|
|
№ п/п |
Этап урока
|
Баллы |
||||||
|
|
1 |
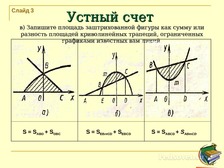
Устный счет |
|||||||
|
|
а) |
|
|||||||
|
|
б) |
|
|||||||
|
|
в) |
|
|||||||
|
|
2 |
Тестовый опрос |
|||||||
|
|
1(А) |
|
|||||||
|
|
2(А) |
|
|||||||
|
|
3(В) |
|
|||||||
|
|
3 |
Нестандартная задача |
|
||||||
|
|
4 |
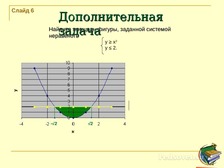
Дополнительная задача |
|
||||||
|
|
Итоговая оценка:
|
||||||||
|
|
Оценочный лист учени(ка)цы 11 класса __________________________________
|
||||||||
|
|
№ п/п |
Этап урока
|
Баллы |
||||||
|
|
1 |
Устный счет |
|||||||
|
|
а) |
|
|||||||
|
|
б) |
|
|||||||
|
|
в) |
|
|||||||
|
|
2 |
Тестовый опрос |
|||||||
|
|
1(А) |
|
|||||||
|
|
2(А) |
|
|||||||
|
|
3(В) |
|
|||||||
|
|
3 |
Нестандартная задача |
|
||||||
|
|
4 |
Дополнительная задача |
|
||||||
|
|
Итоговая оценка:
|
||||||||
Рисунки и задачи взяты из источников:
Лукин Р.Д., Лукина Т.К., Якунина И.С., Устные упражнения по алгебре и началам анализа, М.1989
"Математика для школьников" - научно-практический журнал для школьников, издательство "Школьная пресса"
На странице приведен фрагмент.
|
Автор: Михатова Марина Николаевна
→ Marina2702 |
Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.