Слайд 1
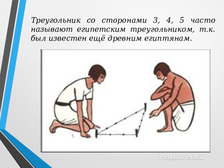
Теорема невест, нимф, бабочки, 100 быков, «бегство убогих», «мост ослов».



























|
Автор: Зудова Светлана Михайловна
→ Публикатор |
Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.

Есть мнение?
Оставьте комментарий