Слайд 1
Презентацию выполнила
учитель математики и
информатики
МБОУ СОШ №10 г.Елабуга РТ.
Саутина Анна Леонидовна
2010 год
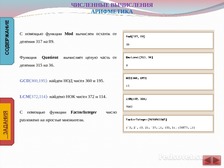
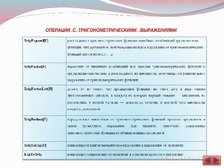
Основной целью использования электронного пособия является формирование у учащихся в систематизированной форме понятия о методах решения задач при использования программного обеспечения компьютера Mathematica 5.0. Учащиеся сначала знакомятся с возможностями пакета, с основными функциями, затем просматривают примеры, самостоятельно работая в программе должны получить такое же решение и ответы, а затем при необходимости из имеющихся в пособии упражнений получают контрольные задания от учителя.

























|
Автор: Саутина Анна Леонидовна
→ Anna9392 |
Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.

Есть мнение?
Оставьте комментарий