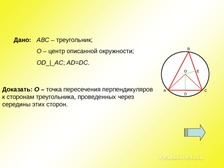
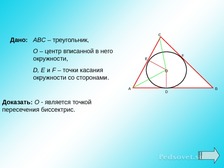
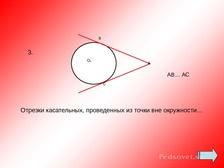
Слайд 48
Много нового появилось со времен Евклида и в самой евклидовой
геометрии. Еще в семнадцатом веке благодаря работам французского математика
и философа Р. Декарта возник метод координат, ознаменовавший собой
революционную перестройку всей математики, и в частности геометрии.
Появилась возможность истолковывать алгебраические уравнения в виде
геометрических образов (графиков) и, наоборот, искать решение геометрических
задач с помощью аналитических формул, систем уравнений.
Так в рамках евклидовой геометрии появилась ее новая ветвь –
аналитической
геометрии,
явившаяся
мощным
средством
исследования
геометрических образов. Например, метод координат позволяет быстро и с
помощью несложных вычислений вывести основные свойства линии второго
порядка (Эллипса, гиперболы, параболы).
Геометрия изучает те свойства фигур, которые сохраняются при движениях.
Иначе говоря, если одна фигура получается из другой движением, то у этих фигур
одинаковые геометрические свойства. В этом смысле движения составляют основу
геометрии.