Презентация "Формулы сокращенного умножения" для 8-11 класса

Слайд 1

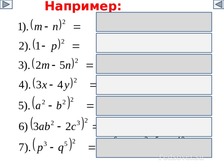
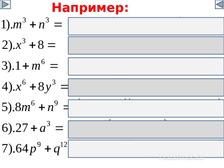
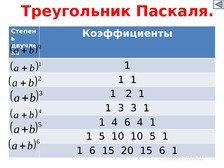
Формулы сокращенного умножения 1) Квадрат суммы. 2) Квадрат разности. 3) Разность квадратов. 4) Куб суммы. 5) Куб разности. 6) Сумма кубов. 7) Разность кубов. 8) Треугольник Паскаля. 9) Бином Ньютона. Учитель МОУ СОШ№5 г. Пролетарска Ростовской обл. Бельмасова Н.И.

Слайд 2

2 2 ( a  b )  a  2 ab  b Квадрат суммы двух чисел равен: квадрату первого числа, плюс удвоенное произведение первого числа на второе, плюс квадрат второго числа. Формула шутка ( + )= = +2 + 2 2

Слайд 3

Например: 1).  m  n   2 2). 1  p   2 2 m  2 mn  n 1 2 p  p 2 2 3).  2m  5n   4 m  20 mn  25 n 2 2 4).  3 x  4 y  2 2  9 x  24 xy  16 y    a  2a b  b 6) 3ab  2c   9 a b  12 ab c p  2 p q  q 7).  p  q   2 5). a  b 2 2 5 2 2 2 3 2 2 3 4 6 2 4 5 2 4 2 3 3 2 10  4c 6

Слайд 4

2 2 ( a  b )  a  2 ab  b 2 Квадрат разности двух чисел равен: квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа. Формула шутка ( - )= -2 + = 2

Слайд 5

Например: 1).  m  n   2 2). 1  p   2 2 m  2 mn  n 1 2 p  p 2 2 3).  2m  5n   4 m  20 mn  25 n 2 2 4).  3 x  4 y  2 2  9 x  24 xy  16 y    a  2a b  b 6) 3ab  2c   9 a b  12 ab c p  2 p q  q 7).  p  q   2 5). a  b 2 2 5 2 2 2 3 2 2 3 4 6 2 4 5 2 4 2 3 3 2 10  4c 6

Слайд 6

a  b   a  b   a  b  2 2 Разность квадратов двух чисел равна: произведению разности этих чисел на их сумму. Формула шутка =( 2 - 2 = . - )( + )

Слайд 7

Например:  y  x   y  x  2 2). 9   3m   3  3m   3  3m  2 2 1). y  x  4 3). 16  p  6 4). 25  a  4 2 5). m  n  4 6). 1  x  8 7). p  49 4  p  4  p  5  a  5  a  m  n  m  n  1  x  1  x   p  7   p  7  2 2 3 2 3 2 2 4 2 4

Слайд 8

3 (a  b)  3 2 2  a  3 a b  3 ab  b Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа на второе, плюс утроенное произведение первого числа на квадрат второго числа, плюс куб второго числа. 3

Слайд 9

Например: 1).  x  y   x 3  3 x 2 y  3 xy 2  y 3 3 2).  a  2   a 3  6a 2  12a  8 3 3).  2a  3b  8a 3  3 4a 2 3b  3 2a 9b 2  27b 3 3 4).  m  4   m 3  3 m 2 4  3 m 16  64 3 5).  x  3 z   x  3 x 3 z  3 x 9 z  27 z 3 3 2 2 6).  2b  3  8b  3 4b 3  3 2b 9  27 3 3 2 7).  n  1  n  3n  3n  1 2 3 6 4 2 3

Слайд 10

3 (a  b)  3 2 2  a  3 a b  3 ab  b 3 Куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого числа на квадрат второго числа минус куб второго числа.

Слайд 11

Например: 1).  x  y   x 3  3 x 2 y  3 xy 2  y 3 3 2).  a  2   a 3  6a 2  12a  8 3 3).  2a  3b  8a 3  3 4a 2 3b  3 2a 9b 2  27b 3 3 4).  m  4   m 3  3 m 2 4  3 m 16  64 3 5).  x  3 z   x 3  3 x 2 3 z  3 x 9 z 2  27 z 3 3 6).  2b  3  8b 3  3 4b 2 3  3 2b 9  27 3 7).  n  1  n  3n  3n  1 2 3 6 4 2

Слайд 12

3 3 a b     a  b   a  ab  b 2 2 Сумма кубов равна произведению суммы этих чисел на неполный квадрат их разности. 

Слайд 13

Например: 3 3 1).m  n   m  n  m 2  mn  n 2 3 2 2).x  8   x  2 x  2 x  4     3).1  m  1  m 1  m  m  4).x  8 y   x  2 y  x  2 x y  4 y  5).8m  n   2m  n  4m  2m n  n  6).27  a   3  a  9  3a  a  7).64 p  q  4 p  q 16 p  4 p q  q  6 2 6 3 6 2 2 9 4 4 2 3 2 4 3 9 2 2 3 6 3 4 8 2 12 3 4 6

Слайд 14

3 3 a  b     a  b   a  ab  b 2 2 Разность кубов равна произведению разности этих чисел на неполный квадрат их суммы. 

Слайд 15

Например: 3 3 2 2 1).m  n   m  n  m  mn  n   x  2 x 3 2).x  8  2  2x  4   1  m 1  m  m  4).x  8 y   x  2 y  x  2 x y  4 y  5).8m  n   2m  n  4m  2m n  n  6).27  a   3  a  9  3a  a  7).64 p  q  4 p  q 16 p  4 p q  q  6 3).1 m  6 3 6 2 2 2 9 4 4 2 3 2 4 3 9 2 2 3 6 3 4 8 2 12 3 4 6

Слайд 16

Треугольник Паскаля. Степен ь двучле 0 на a  b 1 a  b a  b 2 a  b 4  a  b  a  b  a  b 3 5 6 Коэффициенты 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1

Слайд 17

Бином Ньютона.  a b n n  1 n 1 n 2 n 2 2 n n 1 n n 1 n a C a b C a b ...C ab b n! n  n  1... n  k  1 C    n  k  ! k! k! k n

Полный текст материала Презентация "Формулы сокращенного умножения" для 8-11 класса смотрите в скачиваемом файле.
На странице приведен фрагмент.

Автор: Бельмасова Наталья Ивановна → Sigma6413

24.10.2012

7038

2492

Комментировать

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.

Вход | Регистрация

запомнить
Забыл пароль \| Регистрация