Главная → Файлы для скачивания → ЕГЭ → Математика

Презентация "Координатный метод при решении заданий С2 на ЕГЭ" 11 класс


Слайд 1
Лещенко С. И. учитель математики МБОУ СОШ № 8 г. Туапсе Краснодарского края
Слайд 2
Слайд 3
ur p ur p  x1 ; y1 ; z1 r q  x2 ; y2 ; z2  r q а b cos � a, b   -направляющие вектора прямых x1 x2  y1 y2  z1 z2 x y z 2 1 2 1 2 1 x2  y2  z2 2 2 2
Слайд 4
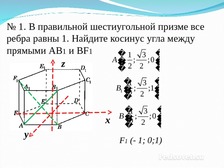
№ 1. В правильной шестиугольной призме все ребра равны 1. Найдите косинус угла между прямыми АВ1 и ВF1 �1 3 � A�  ; ;0 �2 2 � � z � � �1 3 � B1 � �2 ; 2 ;1� � � � х у �1 3 � B� �2 ; 2 ;0 � � � � F1 (- 1; 0;1)
Слайд 5
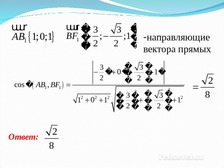
uuur AB1  1;0;1 uuur � 3 3 � BF1 �  ; ;1� -направляющие 2 � �2 вектора прямых � 3� 3  � 1 0 �  1 � � 1 � 2 � 2 � cos � AB1 , BF1   2 1  0 1 2 Ответ: 2 8 2 2 2 � 3� � 3� 2  � �  � 1 � � 2� � 2 � 2  8
Слайд 6
№ 2. Ребро куба равно 4. Найдите косинус угла между прямыми PQ и EF, P – середина АА1, Q – середина С1D1 , Е – серединаz ВВ1, F – середина DC. Q Р (4; 0; 2) uuur PQ  4; 2; 2 Q (0; 2; 4) P F E (4; 4; 2) uuur E у х cos � PQ, EF   1 Ответ: 3 F (0; 2; 0) EF  4; 2; 2 4 �  4   2 �  2   2 �  2  1 2 2 2 2  2 2  4   2  2  4    2    2  3
Слайд 7
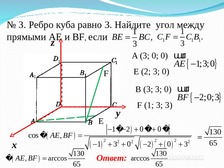
№ 3. Ребро куба равно 3. Найдите угол между 1 1 прямыми AE и BF, если BE  BC , C1 F  C1B1. z 3 3 A (3; 0; 0) uuur Е (2; 3; 0) F AE  1;3;0 В (3; 3; 0) uuur E cos � AE , BF   х � AE , BF   arccos 130 65 BF  2;0;3 F (1; 3; 3) у 1� 3 0� 3  2   0 �  1  3  0 2  2  0  3     130 Ответ: arccos 65 2 2 2 2 2 130  65
Слайд 8
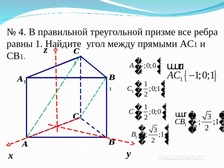
№ 4. В правильной треугольной призме все ребра равны 1. Найдите угол между прямыми AС1 и z С СB1. �1 � 1 A � ; 0;0 � uuuu r �2 � AC1  1;0;1 В А1 1 �1 � C�  ;0;0 � uuur �1 �2 � С А х �1 � C1 �  ;0;1� �2 � 3 � CB1 � ; ;1� � 3 � �2 2 � B1 � 0; ;1� � � � 2 В у �
Слайд 9
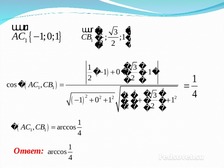
uuuu r AC1  1;0;1 uuur �1 3 � CB1 � ; ;1� �2 2 � �3� 1 � 1  1  0 � � � 1 � 2 �2 � cos � AC1 , CB1    1 1 � AC1 , CB1   arccos 4 Ответ: arccos 1 4 2 2  0 1 2 2 2 �1 � � 3 � 2 � � � � 1 �2 � �2 � 1  4
Слайд 10
Слайд 11
Углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость. α - угол между прямой и плоскостью ur p α β r n sin  sin(90   ) cos  β – угол между прямой и перпендикуляром к плоскости Чтобы найти синус угла между прямой и плоскостью можно найти косинус угла между прямой и перпендикуляром к плоскости
Слайд 12
ax  by  cz  d  0 r n  a; b; c ur p  x1 ; y1 ; z1 r ur   � n, p  sin   уравнение плоскости - вектор нормали к плоскости - направляющий вектор прямой  ax1  by1  cz1 a b c 2 2 2 x y z 2 1 2 1 2 1
Слайд 13
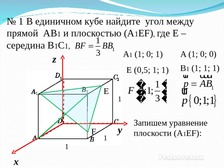
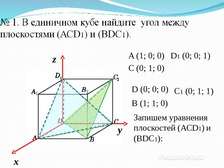
№ 1 В единичном кубе найдите угол между прямой AВ1 и плоскостью (А1EF), где Е – 1 середина В1С1, BF  BB1 3 A1 (1; 0; 1) A (1; 0; 0) z Е (0,5; 1; 1) E F 1 х 1 1 у B1 (1; 1; 1) ur uuur p  AB1 � 1� F� 1;1; � ur � 3 � p  0;1;1 Запишем уравнение плоскости (А1EF):
Слайд 14
A1 (1; 0; 1) � 1� F� 1;1; � � 3� Е (0,5; 1; 1) 4 2 7 cx  cy  cz  c  0 3 3 3 4 2 7 x yz 0 3 3 3 4 x  2 y  3z  7  0 ax  by  cz  d  0 � � acd 0 � 1 � � abcd  0 2 � 1 � ab cd  0 � 3 � - уравнение плоскости (А1EF). � 4 a c � 3 � � 2 b c � � 3 7 � d   c � 3 �
Слайд 15
4 x  2 y  3z  7  0 r n  4; 2;3 ur p  0;1;1 r ur   � n, p  sin    - вектор нормали к плоскости - направляющий вектор прямой 4� 0  2� 1 3� 1 4 2 3 2 5   arcsin 58 2 2 0 1 1 2 2 2 5  58 5 Ответ: arcsin 58
Слайд 16
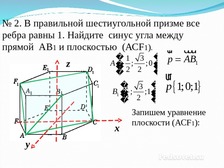
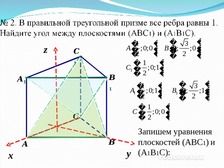
№ 2. В правильной шестиугольной призме все ребра равны 1. Найдите синус угла между прямой AВ1 и плоскостью (АСF1). ur uuur � 1 3 � p  AB 1 A�  ; ;0 � z �2 2 � � � �1 3 � B1 � �2 ; 2 ;1� � � � х у ur p  1;0;1 Запишем уравнение плоскости (АСF1):
Слайд 17
�1 3 � C (1; 0;0) A�  ; ;0 � �2 2 � � � ax  by  cz  d  0 F1 (- 1; 0;1) dx  3dy  2dz  d  0 x  3 y  2z 1  0 - уравнение плоскости (АСF1). �1 3  a bd 0 � 2 2 � � ad 0 � � a  c  d  0 � � a  d � � b   3d � � c  2d �
Слайд 18
x  3 y  2z 1  0 r n 1; 3; 2 - вектор нормали к плоскости   ur p  1;0;1 r ur   � n, p  sin    - направляющий вектор прямой 1� 1 3 � 0  2� 1 2 1  3  22 12  02  12 2 3 Ответ: 4 3  4
Слайд 19
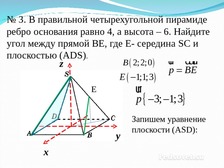
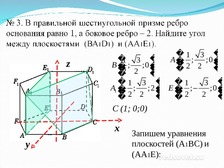
№ 3. В правильной четырехугольной пирамиде ребро основания равно 4, а высота – 6. Найдите угол между прямой ВЕ, где Е- середина SC и плоскостью (АDS). ur uuu r B  2; 2;0  z p  BE E  1;1;3 ur p  3; 1;3 E y х Запишем уравнение плоскости (АSD):
Слайд 20
A  2; 2;0  D  2; 2;0  S  0;0;6  ax  by  cz  d  0 1 1 0dx  dy  dz  d  0 2 6 0x  3y  z  6  0 - уравнение плоскости (АSD). 2a  2b  d  0 � � 2a  2b  d  0 � � 6c  d  0 � � � a0 � � 1 b d � � 2 1 � c d � 6 �
Слайд 21
0x  3 y  z  6  0 r n  0;3; 1 - вектор нормали к плоскости ur p  3; 1;3 r ur   � n, p  sin    - направляющий вектор прямой 3 � 0  3�  1  3 �  1 0  3   1 2 6   arcsin 190 2 2  3 Ответ: 2   1  3 2 6 arcsin 190 2 6  190
Слайд 22
Слайд 23
Угол между плоскостями равен углу между перпендикулярами к этим плоскостям. a1 x  b1 y  c1 z  dуравнение плоскости 1  0 a2 x  b2 y  c2 z  dуравнение плоскости 2  0 r n m a1 ; b1 ; c1   ur m n a2 ; b2 ; c2      cos m;n  a1a2  b1b2  c1c2 2 1 2 1 2 1 a b c 2 2 2 2 a b c 2 2  
Слайд 24
Например:   2 x  3 y  6 zуравнение  5  0  плоскости 4 x  4 y  2 zуравнение  7  0  плоскости ur m  2;3;6   r n  4; 4; 2   uurr cos m;n    4� 2  3� 4  6� 2 22  32  62 42  42  22 16  21
Слайд 25
A (1; 0; 0) D1 (0; 0; 1) C (0; 1; 0) z D (0; 0; 0) C1 (0; 1; 1) B (1; 1; 0) у х Запишем уравнения плоскостей (АСD1) и (BDC1):
Слайд 26
A (1; 0; 0) ax  by  cz  d  0 ad 0 � � bd 0 � � cd 0 � a  d � � b  d � � c  d �  dx  dy  dz  d  0 d 0 � � abd  0 � � bcd  0 � d 0 � � a  b � � c  b � bx  by  bz  0 C (0; 1; 0) D1 (0; 0; 1) D (0; 0; 0) B (1; 1; 0) C1 (0; 1; 1) uu rr cos m;n     ur m  1;1;1   ACD1  x y z 0 r n  1; 1;1   DBC1  1� 1  1� 1  1� 1 1 1 1 2 ur r 1 � m; n  arccos 3  x  y  z 1  0 2 2 1   1  1 2 2 1 Ответ: arccos 3 2 1  3
Слайд 27
z С 1 В А1 1 С А х В �1 � � 3 � A � ;0;0 � B � 0; ;0� � �2 � � 2 � � �1 � C1 �  ; 0;1� �2 � � 3 � �1 � A1 � ; 0;1� B1 � 0; ;1� � � �2 � � 2 � �1 � C�  ;0; 0 � �2 � Запишем уравнения плоскостей (АBС1) и у (A1B1C):
Слайд 28
ax  by  cz  d  0 �1 � A � ; 0;0 � �2 � � 3 � B� 0; ;0 � � � � 2 � �1 � C1 �  ; 0;1� �2 � �1 � A1 � ; 0;1� �2 � � 3 � B1 � 0; ;1� � � 2 � � �1 � C�  ;0;0 � �2 � �1 �2 a  d  0 � �3 � bd 0 �2 �1  acd  0 � �2 �1 �2 a  c  d  0 � �3 � bcd  0 �2 �1  ad 0 � �2 2 dy  2dz  d  0 3 2 2x  y  2z 1  0 3 2dx  a  2d � � 2 � b   d � 3 � r� � c  2 d u � 2 � m� 2; ; 2 �  ABC1  � 3 a  2d � � � 2 b d � 3 � � c  2d � 2 2dx  dy  2dz  d  0 3 2x  2 y  2z 1  0 3 r� 2 � n� 2; ; 2 �  A1 B1C  � 3
Слайд 29
r� 2 � n� 2; ; 2 � � 3 ur � 2 � m� 2; ; 2� � 3 uurr cos m;n    2 2 2� 2 �  2� 2 3 3 2 2 2 �2 � 2 2 �2 � 2  � � 2 2  � �  2  �3� �3� 2 ur r 1 � m; n  arccos 7   1 Ответ: arccos 7 1  7
Слайд 30
z �1 3 � A�  ; ;0 �2 2 � � � � �1 3 � B� �2 ; 2 ;0 � � � � �1 3 � �1 3 � A1 �  ; ;2� E�  ; ;0 � � � � � 2 2 2 2 � � � � C (1; 0;0) х у Запишем уравнения плоскостей (А1BC) и (AA1E):
Слайд 31
ax  by  cz  d  0 � �1 3 B� �2 ; 2 ;0 � � � � �1 3 � A1 �  ; ;2� � � 2 2 � � C (1; 0;0) �1 3 bd 0 � a 2 �2 � 3 �1  a  b  2c  d  0 � 2 �2 ad 0 � � � 1 1 dx  dy  dz  d  0 2 3 1 1 x y  z 1  0 2 3 � � a  d � 1 � b   d � 3 � � 1 c d � � 2 ur � 1 1 � m� 1; ; �  A1 BC  � 3 2
Слайд 32
�1 A�  ; � �2 �1 A1 �  ; � �2 3 � ax  by  cz  d ;0 � 2 � 3 � �1 3 � ;2� 2 � � �1 3 � E�  ; ;0 � � � 2 2 � �  a � �2 � �1  a � �2 �1  a � �2 2dx  0 � y  0� zd 0 2x  0 � y  0� z 1  0 r n  2; 0; 0   A1 AE  bd 0 2 3 b  2c  d  0 2 3 bd 0 2 0 a  2d � � b0 � � c0 �
Слайд 33
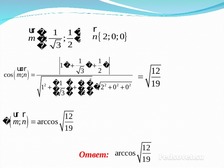
ur � 1 1 � r m� 1; ; � n  2; 0; 0 � 3 2 uu rr cos m;n    1 1 1� 2 � 0 � 0 2 3 2 2 �1 � �1 � 12  � � � ��22  02  02 � 3 � �2 � 12  19 ur r 12 � m; n  arccos 19   12 Ответ: arccos 19
Слайд 34
Литература : Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения. МАТЕМАТИКА ЕГЭ 2011 (типовые задания С2) 18.02.2011 http://alexlarin.net/ege11.html
Слайд 1
Лещенко С. И. учитель математики МБОУ СОШ № 8 г. Туапсе Краснодарского края
Слайд 2
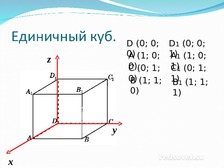
Слайд 3
D (0; 0; D1 (0; 0; 0) A (1; 0; 1) A1 (1; 0; 0) C (0; 1; 1) C1 (0; 1; 0) B (1; 1; 1) B1 (1; 1; 0) 1) z у х
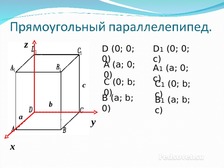
Слайд 4
z D (0; 0; 0) A (a; 0; 0) C (0; b; 0) B (a; b; 0) c b a х у D1 (0; 0; c) A1 (a; 0; c) C1 (0; b; c) B1 (a; b; c)
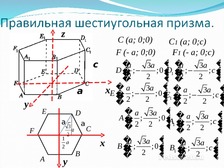
Слайд 5
z C (a; 0;0) F (- a; 0;0) �a D� �2 ;  � � хE � a ;  �2 � 3a � �a ;0 � D1 � ; � � 2 � �2 3a � � a ;0 � E1 �  ; � � 2 ��2 � a 3a � � a A�  ; ;0 � A1 �  ; �2 2 � � � ��2 c a у E a 3 a 2 1 a 2 F A у D a C х B C1 (a; 0;c) F1 (- a; 0;c) 3a � ;c� � 2 � 3a � ;c� � 2 � 3a � ;c � � 2 � �a 3a � �a 3a � B� ; ;c� �2 ; 2 ;0 � � B1 � � � � � �2 2 �
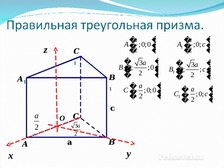
Слайд 6
z С 1 А1 a 2 А х �a � A � ;0;0 � �2 � С O � 3a � � 3a � B� 0; ;0 � 0; ;c� � 2 � B1 � � � 2 � � � � В �a � 1 a � C�  ;0;0 � C �  ;0; c 1� � �2 � 2 � � c 3a 2 a �a � A1 � ;0; c � �2 � В у
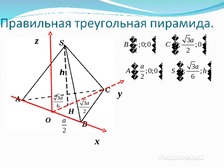
Слайд 7
� 3a � �a � B � ;0;0 � C � 0; ;0 � � � 2 �2 � � � z �a � � 3a � A�  ; 0;0 � S � 0; ;h� � � �2 � � 6 � h 3a 6 O y H 3a 2 a 2 х
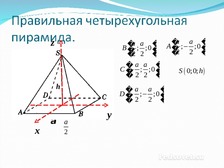
Слайд 8
z �a a � A �a ;  a ; 0 � B � ; ;0 � � � 2 2 � � �2 2 � �a a � C�  ; ;0 � S  0;0; h  2 2 � � h h х �a a � D�  ;  ;0 � �2 2 � a a 2 y
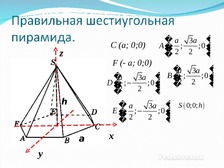
Слайд 9
C (a; 0;0) z F (- a; 0;0) � a 3a � A�  ; ;0 � � � 2 2 � � �a 3a � ; ;0 � �a 3a � B � � � 2 2 D� ;  ;0 � � � �2 � 2 � � h �a 3a � S  0;0; h  E�  ; ;0 � � � 2 2 � � a y х
Слайд 10
Слайд 11
  M ;   ax0  by0  cz0  d a b c 2 Например: M  3;1; 2    M ;   2 2 3 x  4 y  12 z  2  0 3� 1  12 � 22  3  4 � 3  4   12  2 2 2 27  13
Слайд 12
M  xm ; ym ; zm  N  xn ; yn ; zn  P  xp ; yp ; z p  Уравнение плоскости имеет вид ax  by  cz  d  0 Числа a, b, c находим из системы уравнений � axm  bym  czm  d  0 � axn  byn  czn  d  0 � � ax p  by p  cz p  d  0 �
Слайд 13
Например: Написать уравнение плоскости, проходящей через точки M  0;1;0  N  1;0; 0  ax  by  cz  d  0 bd 0 � � ad 0 � � abcd  0 � P  1;1;1 a� 0b� 1 c � 0d  0 � � a� 1 b � 0c� 0d  0 � � a� 1 b � 1 c � 1 d  0 � b  d � � a  d � � d  d  c  d  0 � b  d � � a  d � � cd � dx  dy  dz  d  0 :  d  - уравнение плоскости, проходящей x  y  z  1  0 через три данные точки.
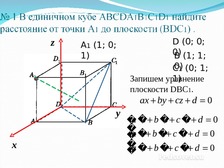
Слайд 14
z A1 (1; 0; 1) D (0; 0; 0) B (1; 1; C0) 1 (0; 1; 1) Запишем уравнение плоскости DBC1. ax  by  cz  d  0 у х a� 0b� 0c� 0d  0 � � a� 1 b � 1 c � 0d  0 � � a� 0b� 1 c � 1 d  0 �
Слайд 15
d 0 � � abd  0 � � bcd 0 � d 0 � � a  b � � c  b � bx  by  bz  0 x yz 0 A1 (1; 0; 1) Найдем искомое :  b  расстояние по формуле   M ;   ax0  by0  cz0  d 1� 1  1� 0  1� 1 a b c 2 2 2 2 2 3   A1 ;( BC1 D)     2 2 2 3 3 1  (1)  1 2 3 Ответ: 3
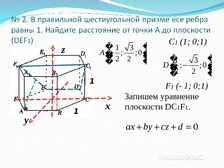
Слайд 16
�1 3 � A�  ; ;0 � � � 2 2 � � z 1 у 1 х C1 (1; 0;1) �1 3 � D� �2 ;  2 ;0 � � � � F1 (- 1; 0;1) Запишем уравнение плоскости DC1F1. ax  by  cz  d  0
Слайд 17
� a� 1 b � 0c� 1 d  0 acd  0 � � � � 3� 3 �1 � 1 a bd 0 a� b�   c � 0  d  0 � � � � � 2 � 2 2 �2 � � � a  c  d  0 � � a� 0c� 1 d  0 �  1  b � � � � a0 2 � � 0 � x  dy  dz  d  0 :d c   d � 3 � 2 � b d 2 � 3 y  z 1  0 3
Слайд 18
Найдем искомое ax0  by0  cz0  d расстояние по формуле   M ;    a 2  b2  c 2 2 0� x y  z 1  0 3   A;  DC1 F1    3 �1� 2 0�  � �  1� 0 1 � � 2� 3 2 2 2 �2 � 0  � �  1 �3� 2 2 3 Ответ: 7 �1 3 � A�  ; ;0 � � � 2 2 � � 2 3  7
Слайд 19
Слайд 20
Расстоянием между скрещивающимися прямыми называется расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через вторую прямую, параллельно первой. b A  B c b P   b; c     b;      A;  
Слайд 21
z AD1 P BC1 AD1 P( DBC1 )   AD1 ; BD   у х   AD1 ;  BDC1      A;  BDC1  
Слайд 22
D (0; 0; Запишем уравнение 0) плоскости BDC1. B (1; 1; C0) 1 (0; 1; ax  by  cz  d  0 1)0 a � 0  b � 0  c � 0  d  � d 0 � A (1; 0; 0) � a� 1 b � 1 c � 0d  0 � � a� 0b� 1 c � 1 d  0 � � a  b � � c  b � bx  by  bz  0 x yz 0   M ;   Найдем искомое расстояние по формуле ax0  by0  cz0  d a b c 2 2 2
Слайд 23
A (1; 0; 0) x yz 0 1� 1  1� 0  1� 0 1 3   A;( BC1D )     2 2 2 3 3 1  (1)  1 3 Ответ: 3
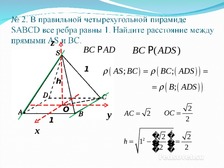
Слайд 24
z BC P AD 1 h х   AS ; BC     BC ;  ADS       B;  ADS   O 1 BC P( ADS ) y AC  2 2 OC  2 2 �2� 2 h  1 � �2 � � 2 � � 2
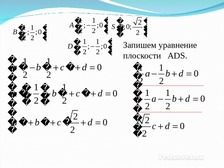
Слайд 25
�1 1 � B � ; ;0 � �2 2 � �1 1 � � 2� A � ;  ;0 �S � 0; 0; � � 2 2 � � � 2 � � � 1 1 � Запишем уравнение D�  ;  ;0 � �2 2 � � 1 1 a�b� c� 0d  0 � 2 � 2 � � 1� 1 a�  � b �  c � 0d  0 � � � � 2� 2 � 2 � a� 0b� 0c�  d  0 � 2 плоскости ADS. �1 1 �2 a  2 b  d  0 � 1 �1  a bd 0 � 2 �2 �2 � cd 0 �2
Слайд 26
� a0 � b  2d � � c   2d � 0� x  2dy  2dz  d  0 : d 0� x  2 y  2z 1  0 Найдем искомое расстояние по формуле �1 1 � B � ; ;0 � �2 2 �   B;( ASD)   Ответ: 6 3   M ;   ax0  by0  cz0  d a 2  b2  c 2 1 1 0�  2�  2 � 0 1 2 2  0 2   2 2 2  2 2 6   3 6
Слайд 27
Литература : Корянов А.Г., Прокофьев А.А. Многогранники: виды задач и методы их решения. МАТЕМАТИКА ЕГЭ 2011 (типовые задания С2) 18.02.2011 www.alexlarin.narod.ru

Полный текст материала Презентация "Координатный метод при решении заданий С2 на ЕГЭ" 11 класс смотрите в скачиваемом файле.
На странице приведен фрагмент.
Автор: Лещенко Светлана Ивановна →  ячс8190
30.01.2013 2 16214 3522

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.


А вы знали?
Как не реагировать на негатив? Почему меня ранит критика и высказывания других людей
Шесть советов, как запустить сарафанное радио репетиторам и экспертам

Инструкции по ПК
Как оплатить ZOOM из России в 2023 году? Как оплатить и другие зарубежные сервисы, заблокированные из-за «санкций»?
Как работать в Canva в России после 01.06.22. Через какой VPN открыть Canva на компьютере?