Разработка урока математики "Решение задач C1"; 11 класс

МОУ Дмитровская СОШ№10

Решение задач С1

Урок алгебры в 11 классе

Учитель математики Елакова Л.Л.

Цели урока:

Обучающие - повторить различные типы тригонометрических уравнений; отработать навыки нахождения корней уравнений на тригонометрическом круге; сформировать умение отбирать корни тригонометрических уравнений на отрезке.

Развивающие - развивать логическое мышление через умение обобщать, доказывать и опровергать.

Воспитательные - воспитание настойчивости в приобретении знаний и умений, умение принимать самостоятельные решения.

Методические - показать различные формы и методы контроля и самоконтроля качества знаний, умений и навыков учащихся.

Тип урока: урок применения знаний и умений.

Ход урока:

1.Организационный этап.

Сегодня на уроке мы разберем некоторые приемы решения задач С1, определим алгоритм решения уравнений с отбором корней на отрезке, чтобы на ЕГЭ без ошибок справиться с заданиями такого типа.

2.Устная работа.

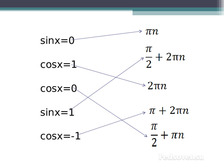
Задание 1. На доске слайд со следующим текстом

0

1 + 2

= 0 2

1 + 2

-1 +

Назовите выражение из второго столбца, которое соответствует уравнению из первого столбца. Учащиеся объясняют свой выбор с помощью тригонометрического круга.

Задание 2. На доске слайд с таблицей , в которой только левый столбец. Учащиеся вспоминают формулы корней тригонометрических уравнений. По щелчку появляется соответствующая формула.

Вид уравнения	Общая формула решения
а, |a|≤1	arcsin а + , k€Z
= а, |a|≤1	± a + 2 , k€Z
a	a + , k€Z
a	a + , k€Z

Задание 3. На доске задание со следующим текстом.

1. 2 1

2. -2 1

4. -

5. =

С помощью тригонометрического круга решить уравнения. На доске появляется слайд с правильными ответами. Учащиеся отмечают, сколько заданий они выполнили правильно.

Задание 4. Знание тригонометрических формул применяется при решении уравнений. Приготовимся к математическому диктанту по вариантам.

1в. 2в.

1 - 1 -

- 2

На доске появляется слайд с ответами. Учащиеся меняются тетрадями и проверяют работу соседа.

Задание 5. Вспомним различные виды тригонометрических уравнений. Учащиеся называют – учитель помогает.

3. Решение уравнений.

1. 2 + - 2 = 0

Учащиеся предлагают способ решения и решают на доске.

Вместе с учителем на тригонометрическом круге выполняем дополнительные задания. Найти корни уравнения на отрезке [0; ]; на отрезке [ ; ]; на отрезке [ 2 ].

2. – = 0

Учащимся предлагается на доске решить уравнение двумя способами. Вместе определяем, как объединить группы корней уравнения в одну и записываем ответ. С помощью тригонометрического круга учащиеся предлагают отобрать корни на отрезках:

[ 2 ]; [ ; ]; [ ; ].

4. Самостоятельная работа.

Учащиеся разбиваются на 5 групп по 4-5 человек. Каждой группе дается одно уравнение с отбором корней. Сильные ученики, решив уравнение, становятся консультантами своей группы.

1.Решите уравнение + .

Укажите корни, принадлежащие отрезку [ ].

2.Решите уравнение = 0.

Укажите корни, принадлежащие отрезку [ ].

3.Решите уравнение = 0.

Укажите корни, принадлежащие отрезку

[ ].

4.Решите уравнение = 0.

Укажите корни, принадлежащие отрезку

[ ].

5.Решите уравнение = 0.

Укажите корни, принадлежащие отрезку

[ ].

5. Итог урока.

Консультанты оценивают учащихся своих групп. Учитель с помощью учащихся определяет алгоритм решения уравнений с отбором корней.

На следующих занятиях мы разберем другие виды уравнений с отбором корней.

6.Задание на дом.

1.Решите уравнение + - =0 и укажите корни, принадлежащие отрезку [ ].

2.Решите уравнение - (4 - 3 ) + 2 (1 - ) =0 и укажите корни, принадлежащие отрезку [ ]