Урок + презентация по математике по теме "Треугольник. Свойства углов треугольника" для 5 класса

Щербакова Надежда Валериевна

учитель математики и информатики МОУ гимназии № 30 г. Ульяновска

Урок математики в 5 классе

«Треугольник. Свойства углов треугольника»

«Я слышу – я забываю, я вижу – я запоминаю, я делаю – я усваиваю»

Китайская мудрость

Как известно, в основе нынешней модернизации российского образования лежат идеи личностно-ориентированного развивающего обучения. Сегодня одна из важнейших задач общеобразовательной школы состоит уже не в том, чтобы «снабдить» учащихся багажом знаний, а в том, чтобы привить умения, позволяющие им самостоятельно добывать информацию и активно включаться в творческую, исследовательскую деятельность. В связи с этим актуальным становится внедрение в процесс обучения таких технологий, которые способствовали бы формированию и развитию у учащихся умения учиться, учиться творчески и самостоятельно.

Основу концепции деятельностного подхода к обучению составляет положение: усвоение содержания обучения и развитие ученика происходит в процессе его собственной деятельности.

Давно доказано психологами, что люди лучше усваивают то, что обсуждают с другими, а лучше всего помнят то, что объясняют другим. И ведь именно эти возможности предоставляет учащимся используемая на уроке учителем групповая работа.

Цель:

• Определить виды треугольников;

• Повторить правила нахождения периметра;

• Вывести свойства углов треугольника;

• Сформировать умение использовать эти свойства при решении задач.

Ход урока

I. Организационный момент …

II. Актуализация знаний

1. С помощью какого инструмента можно измерить углы треугольника?

2. А у любого ли треугольника можно измерит углы?

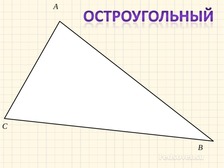
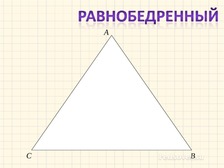
3. Примеры различных треугольников

Эмоциональное включение учащихся в урок

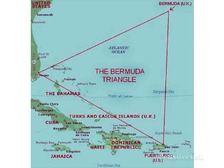
В Атлантическом океане есть место, по форме напоминающее геометрическую фигуру, о которой мы сегодня будем говорить. Это место, расположенное между Бермудскими островами, государством Пуэрто-Рико, полуостровом Флорида и называется “бермудским треугольником”. А ещё его называют “дьявольский треугольник”, “треугольник проклятых”. Загадочность его заключается в том, что в нём бесследно исчезают корабли и самолёты. Природа “бермудского треугольника” остаётся тайной и по сей день.

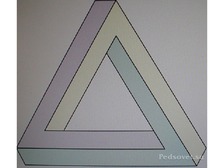
Ещё один общеизвестный треугольник – это «невозможный треугольник». Который увековечен в виде скульптуры в д. Опховен, Бельгия. И треугольник Пенроуза в городе Перт, Австралия.

Треугольник Пенроуза в городе Перт, Австралия.

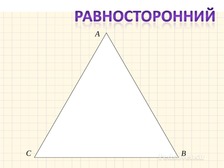
Но мы с Вами поговорим о ВОЗМОЖНЫХ треугольниках. Вспомним виды треугольников

Ты на него, ты на меня,
На всех нас посмотри.
У нас всего, у нас всего,
У нас всего по три.
Три стороны и три угла
И столько же вершин.
И трижды-трудные дела
Мы трижды совершим.

Часто знает и дошкольник,

Что такое треугольник.

А уж вам- то, как не знать …

Но совсем другое дело –

Очень быстро и умело

Величины все улов

в треугольнике узнать.

Поэтому тема сегодняшнего урока «Сумма углов треугольника». Для этого скажите мне, пожалуйста, что такое треугольник? (Треугольник - это фигура, образованная тремя точками, не лежащих на данной прямой, и отрезками, попарно соединяющими эти точки.)

Треугольники различают (называют, то есть классифицируют) по сторонам и по углам. Какие вы знаете треугольники? Сначала вспомним о том, как измеряются углы. Итак:

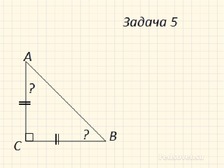
Дело 1. Самостоятельная работа «Измерение углов»

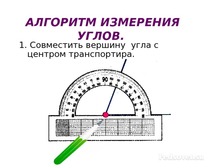
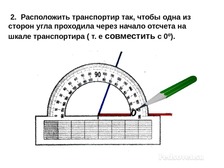
1. Напомнить об алгоритме измерения углов.

2. На экран проецируются различные углы

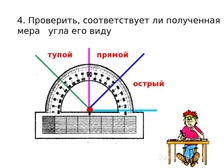
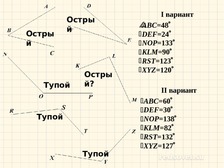
3. Определить вид каждого угла

4. Определить градусную меру угла (задание по вариантам, работа в парах)

III. Этап объяснения нового материала (работа в парах):

Дело 2. Чему равна сумма углов треугольника?

1. На каждую парту раскладываются модели различных треугольников с опросными листами.

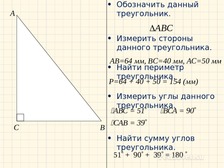
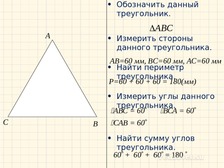
2. Выполнить задания:

   1. Обозначить треугольники

   2. Измерить стороны треугольника

   3. Найти периметр треугольника

   4. Измерить углы треугольника

   5. Найти сумму углов треугольника

Тема: «Треугольники. Свойства углов треугольника»

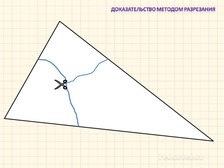
Чему равна сумма углов треугольника? (Оторвем углы треугольника и сложим их вместе, получим развернутый угол. Измеряя мы получили приближенные значения, а в любом треугольнике сума углов равна точно 180)

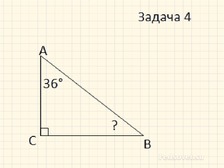
• Чему равна сумма острых углов треугольника?

• Могут ли в треугольнике быть два тупых угла?

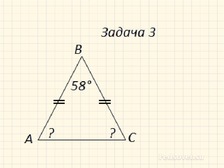
• Чему равен угол равностороннего треугольника?

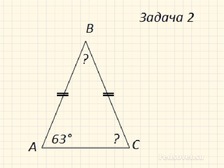
• Чему равны углы при основании равнобедренного треугольника?

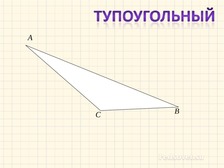
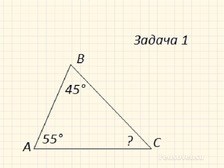
• Может ли треугольник, в котором два угла 40 и 60, быть тупоугольным?

• Может ли треугольник с градусными мерами углов 10 и 20 быть остроугольным?

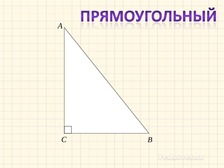
• Является ли треугольник прямоугольным, если градусные меры двух углов 35 и 55?

IV. Закрепление нового материала:

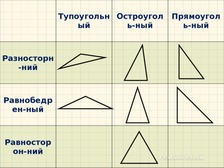
Дело 3. Сообразим-вообразим

Заполнить таблицу

V. Подведение итогов.

Домашнее задание:

1. Учебник п. 31, 32

2. Что такое ФЛЕКСАГОН? Как он строится? Построить его.

3. № 585, 586

VI. Источники материалов.

1. Математика. 5 класс: поурочные планы по учебнику И.И. Зубаревой, А.Г. Мордковича (авт.-сост. Е.А. Ким). – Волгоград: Учитель, 2008.

2. Математика. 5-6 кл.: Методическое пособие для учителя / И.И. Зубарева, А.Г. Мордкович. – 2-е изд. – М.: Мнемозина, 2008.

3. Математика: 5 класс / И. И. Зубарева, А. Г. Мордкович. – М.: Мнемозина, 2009.

4. http://sceptic-ratio.narod.ru/po/kn2.htm

5. http://www.insidepro.com/kk/291/291r.shtml

6. http://www.shahty.ru/blog/blog_84.html

7. http://www.100mat.ru/ubb/viewalbum.php?Cat=&Album=208&page=2

8. http://m.allmystic.ru/page/7080

9. http://noterror.ru/tag/ostrov/