Презентация по информатике "Основы логики и логические основы компьютера."

Слайд 1

Основы логики и логические основы компьютера. Формы мышления.

Слайд 2

 Логика –это наука о формах и способах мышления;особая форма мышления.  Понятие - это форма мышления, фиксирующая основные, существенные признаки объекта.  Высказывание – форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание может быть либо истинно, либо ложно.

Слайд 3

Логика Высказывания:  Истинные(1) и ложные (0);  Простые и сложные;  Общие, частные и единичные.

Слайд 4

Высказывания. • Высказывания бывают общими, частными или единичными. Общее высказывание начинается (или можно начать) со слов: все, всякий, каждый, ни один. Частное высказывание начинается ( или можно начать) со слов: некоторые, большинство и т.п. Во всех других случаях высказывание является единичным.

Слайд 5

Примеры высказываний: Пример 1. Определить тип высказывания (общее, частное, единичное). • «Все рыбы умеют плавать». Ответ: общее высказывание. • «Некоторые медведи -бурые». Ответ: частное высказывание. • «Буква А – гласная». Ответ: единичное высказывание.

Слайд 6

Примеры высказываний: Пример 2. Из двух простых высказываний постройте сложное высказывание, используя логические связки «И», «ИЛИ»: Все ученики изучают математику. Все ученики изучают литературу. Все ученики изучают математику и литературу.

Слайд 7

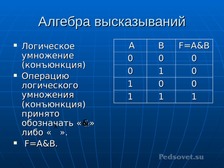
Алгебра высказываний    Логическое умножение (конъюнкция) Операцию логического умножения (конъюнкция) принято обозначать «&» либо «  ». F=A&B. A 0 0 1 1 B 0 1 0 1 F=A&B 0 0 0 1

Слайд 8

Логическое сложение Дизъюнкция Истинно тогда, когда истинно хотя бы одно из входящих в него простых высказываний. F=A  B A 0 0 1 1 B 0 1 0 1 F=A B 0 1 1 1

Слайд 9

Логическое отрицание. A F= A 0 1 1 0 • Таблица истинности логического отрицания. • Инверсия • Делает истинное высказывание ложным и, наоборот, ложное – истинным.

Слайд 10

Логические законы и правила преобразования логических выражений.   Закон тождества. Всякое высказывание тождественно самому себе. Закон непротиворечия.  А=А  А&A=0

Слайд 11

Логические законы и правила преобразования логических выражений.    Закон исключения третьего. Закон двойного отрицания. Закон де Моргана.  А A =1 А А А  В А & В A & B A  B

Слайд 12

Логические законы и правила преобразования логических выражений.  Закон коммутативности. В алгебре высказываний можно менять местами логические переменные при операциях логического умножения и логического сложения: Логическое умножение Логическое сложение А & B B & A А  B A  B

Слайд 13

Логические законы и правила преобразования логических выражений. • Закон ассоциативности. Если в логическом выражении используются только операция логического умножения или только операция логического сложения, то можно пренебрегать скобками или произвольно их расставлять: Логическое умножение Логическое сложение ( A & B) & C  A & ( B & C ) ( A  B)  C  A  ( B  C )

Слайд 14

Логические законы и правила преобразования логических выражений  Закон дистрибутивности. В алгебре высказываний можно выносить за скобки как общие множители, так и общие слагаемые: Дистрибутивность умножения относительно сложения ab+ac=a(b+c) – в алгебре ( A & B)  ( A & C )  A & ( B  C ) Дистрибутивность сложения относительно умножения ( A  B) & ( A  C )  A  ( B & C )

Слайд 15

Логические основы устройства компьютера Базовые логические элементы.  Логический элемент «И» - логическое умножение.  Логический элемент «ИЛИ» - логическое сложение.  Логический элемент «НЕ» - инверсия.

Слайд 16

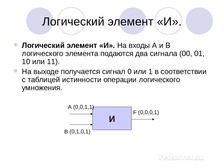
Логический элемент «И».   Логический элемент «И». На входы А и В логического элемента подаются два сигнала (00, 01, 10 или 11). На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности операции логического умножения. А (0,0,1,1) И В (0,1,0,1) F (0,0,0,1)

Слайд 17

Логический элемент «ИЛИ».   На входы А и В логического элемента подаются два сигнала (00, 01, 10 или 11). На входе получается сигнал 0 или 1 в соответствии с таблицей истинности операции логического сложения. А (0,0,1,1) ИЛИ В (0,1,0,1) F (0,1,1,1)

Слайд 18

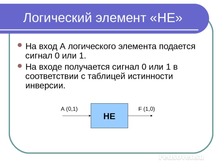
Логический элемент «НЕ»  На вход А логического элемента подается сигнал 0 или 1.  На входе получается сигнал 0 или 1 в соответствии с таблицей истинности инверсии. А (0,1) НЕ F (1,0)

Слайд 19

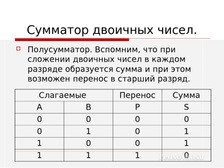
Сумматор двоичных чисел.  Полусумматор. Вспомним, что при сложении двоичных чисел в каждом разряде образуется сумма и при этом возможен перенос в старший разряд. Слагаемые А В 0 0 0 1 1 0 1 1 Перенос Р 0 0 0 1 Сумма S 0 1 1 0

Слайд 20

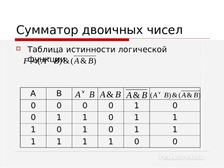
Сумматор двоичных чисел  Таблица истинности логической Fфункции ( A  B ) & ( A & B ) А 0 0 1 1 В 0 1 0 1 А В А& В А& В 0 1 1 1 0 0 0 1 1 1 1 0 ( A  B) & ( A & B) 0 1 1 0

Слайд 21

Полный однозарядный сумматор.   Полный однозарядный сумматор должен иметь три входа: А,В- слагаемые и Р0 – перенос из младшего разряда и два выхода: сумму S и перенос Р. Идея построения полного сумматора точно такая же, как и полусумматора. Перенос реализуется путем логического сложения результатов попарного логического умножения входных переменных. Формула переноса получает следующий вид: Р ( А & B)  ( A & P0 )  ( B & P0 )

Слайд 22

Многозарядный сумматор. • Многозарядный сумматор процессора состоит из полных однозарядных сумматоров. • На каждый разряд ставится однозарядный сумматор, причем выход (перенос) сумматора младшего разряда подключается ко входу сумматора старшего разряда.

Слайд 23

Триггер. • Важнейшей структурной единицей оперативной памяти компьютера, а также внутренних регистров процессора является триггер. Это устройство позволяет запоминать, хранить и считать информацию. S(1) 1 1 0 НЕ ИЛИ 0 ИЛИ R 0 1 НЕ Q

Полный текст материала Презентация по информатике "Основы логики и логические основы компьютера." смотрите в скачиваемом файле.
На странице приведен фрагмент.

Автор: Трегубова Ольга Ивановна → Ольг

19.07.2009

14525

4899

Комментировать

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.

Вход | Регистрация

запомнить
Забыл пароль \| Регистрация