Презентация к уроку "Равносильность неравенств на множествах. Другие преобразования неравенств"

Слайд 1

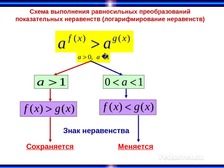
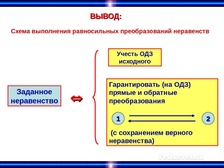
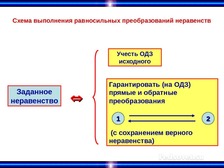
Почему понятие следствия при решении неравенств не используется? Множеством решений неравенства является промежуток или объединение нескольких промежутков, а сделать проверку для всех чисел из этого множества практически невозможно. Какие неравенства называют равносильными на некотором множестве? Два неравенства называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же решения, т.е. каждое решение первого неравенства являются решением второго, и, наоборот.

Слайд 2

Метод решения хорош, если с самого начала мы можем предвидеть – и в последствии подтвердить это, - что, следуя этому методу, мы достигнем цели. Г. Лейбниц

Слайд 3

Схема выполнения равносильных преобразований некоторых иррациональных неравенств 2 k 1 f ( x)  g ( x) f ( x)  g ( x)  2 k 1 2 k 1 f ( x)  g ( x) f ( x )  g ( x )  Знак неравенства сохраняется 2 k 1

Слайд 4

f ( x)  g ( x) 2k g ( x) 0, f ( x)   g ( x)  2k 2k или f ( x) 0, g ( x)  0 f ( x)  g ( x) f ( x) 0, g ( x)  0, f ( x)   g ( x)  2k

Слайд 5

2k f ( x)  2 k g ( x) f ( x)  g ( x), g ( x ) 0

Слайд 6

Схема выполнения равносильных преобразований неравенств, содержащих знак модуля f ( x)  g ( x) f ( x)   g ( x) или f ( x)  g ( x) f ( x)  g ( x) f ( x)   g ( x), f ( x)  g ( x)

Слайд 7

Схема выполнения равносильных преобразований показательных неравенств (логарифмирование неравенств) a f ( x) a g ( x) a  0, a �1 a 1 f ( x)  g ( x) 0  a 1 f ( x)  g ( x) Знак неравенства Сохраняется Меняется

Слайд 8

Схема выполнения равносильных преобразований логарифмических неравенств (потенцирование неравенств) log a f ( x)  log a g ( x) a  0, a �1 a 1 0  a 1 f ( x)  0, g ( x)  0, f ( x)  0, g ( x)  0, f ( x)  g ( x) f ( x)  g ( x) Знак неравенства Сохраняется Меняется

Слайд 9

ВЫВОД: Схема выполнения равносильных преобразований неравенств Учесть ОДЗ исходного Заданное неравенство  Гарантировать (на ОДЗ) прямые и обратные преобразования 1 (с сохранением верного неравенства) 2

Слайд 10

1. Решите неравенство: log 7 ( x  3)  1 (- 3 ; 4) 2х 1 3 1  9 [- 0,5; +) 2. Найдите область определения функции y  log 9 x  2 12 [ 81; + ) 1 y    2 5  10 x [ 0,1; + )  1 16

Слайд 11

РАНОСИЛЬНОСТЬ НЕРАВЕНСТВ НА МНОЖЕСТВАХ. ДРУГИЕ ПРЕОБРАЗОВАНИЯ НЕРАВЕНСТВ

Слайд 12

Схема выполнения равносильных преобразований неравенств Учесть ОДЗ исходного Заданное неравенство  Гарантировать (на ОДЗ) прямые и обратные преобразования 1 (с сохранением верного неравенства) 2

Слайд 13

1. Приведение подобных членов неравенства ( x  1) 2  5 x 2  3 x  2 x Решение: x 0, ( x  1) 2  5 x 2  3 x  2 x 1). x  2 x 1  5 x 2  3x  2 x x 0, ( x  0,2)( x  1)  0 5 x 2  3x  2 x  x  2 x  1  0 + 5x 2  4x  1  0 2 5 x  4 x  1 5( x  0,2)( x  1) -0,2 0 [ 0 ; 1) Ответ: [ 0 ; 1) + 1 х

Слайд 14

2. Применение некоторых формул log 2 x  log 2 ( x  4)  2 Решение: 1). x  0, x   4, x( x  4)  4 x2  4x  4 x2  4x  4  0 log 2 x( x  4)  log 2 4 x 2  4 x  4  ( x  ( 2  8 ))( x  ( 2  8 )) x  0, x   4, ( x  ( 2  8 ))( x  ( 2  8 ))  0 +  2 8 -4 Ответ: + 0  2 8 (0; 2  8 ) х

Слайд 15

Применение знаний и способов действий № 9.37 (а), № 9.39 (а) САМОСТОЯТЕЛЬНАЯ РАБОТА Задание №1 Задание № 2 Задание № 3 № 9.37 (г), № 9.38 (а), № 9.40* (г), № 9.39 (г) № 9.40* (а) № 9.41* (а)

Слайд 16

ДОМАШНЕЕ ЗАДАНИЕ 1. п. 9.5, № 9.38 (б), № 9.39 (б), № 9.40 (б) 2. Дополнительно: 1. На «4»: C1 Найдите наибольшее значение функции f ( x) 3(2 x  6) 4  (2 x  6) 5 при x  3 1 . 2. На «5»: C3 Найдите все значения a, при каждом из которых неравенство a  (3 cos x  1  1) 3 x   3 10 3  x  4  a 0 не имеет решений.

Слайд 17

Полный текст материала Презентация к уроку "Равносильность неравенств на множествах. Другие преобразования неравенств" смотрите в скачиваемом файле.
На странице приведен фрагмент.

Автор: Косолапова Елена Васильевна → ekosolapova

16.03.2009

13778

2241

Комментировать

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.

Вход | Регистрация

запомнить
Забыл пароль \| Регистрация