Урок "Многоугольники и многогранники"

Муниципальное бюджетное общеобразовательное учреждение

«Средняя общеобразовательная школа № 2

с углублённым изучением отдельных предметов»



143968, Московская область, г. Реутов, ул. Победы, д. 32,

тел./факс: (495) 528-03-73, тел.: 528-50-53, e-mail: school2reut@mail.ru

Изучение понятия многогранник в начальных классах

Работу выполнила:

Цирушкина Светлана Александровна

Учитель начальных классов

Реутов 2013

Содержание

Введение………………………………………………………………...……3

Глава I(теоретическая) Изучение понятия многогранник в начальных классах………..………………………………………6

1.1.Психологические особенности детей младшего школьного возраста………………………………………………………………..6

1.2.Понятие как форма абстрактного мышления…………..……….12

1.3Геометрическое определение понятия «многогранник»………17

1.4.Обучение геометрии в начальных классах……………………..19

1.4.1.Анализ учебно-методических комплексов…………….22

Глава II (практическая) Развитие умения использовать логические приёмы при формировании понятия «многогранник» у четвероклассников с использованием компьютера.…..................25

2.1.Выявление уровня знаний о понятиях многогранник и многоугольник у учеников 4-х классов (констатирующий этап)………………………………………………..…………………..25

2.2.Формирующий этап……………………..………………….……32

2.3. Выявление уровня знаний о понятиях многогранник и многоугольник у учеников 4-х классов (контрольный этап)……..….………………………………………………………….42

2.4.Анализ проведённых исследований…..…………………......….45

Заключение и методические рекомендации………………………………47

Список литературы…………………………………………………...…….50

Приложение.

Введение.

В последние годы наметилась тенденция к включению значительного по объёму геометрического материала в начальный курс математики. Но для того, чтобы учитель мог познакомить учащихся с различными геометрическими понятиями (как плоскости, так и пространства), мог научить их правильно изображать геометрические фигуры, ему нужна соответствующая математическая подготовка. Безусловно, нужны знания об истории возникновения и развития геометрии, так как ученик в процессе развития геометрических представлений проходит, в свёрнутом виде, основные этапы создания геометрической науки. Учитель должен быть знаком с ведущими идеями курса геометрии, знать основные свойства геометрических фигур, уметь их построить.

Преподавание геометрии в школе имеет целью не только сообщать учащимся геометрические знания, но и научить их умению логически рассуждать, поэтому геометрия даёт нам лучшие возможности для развития абстрактного мышления в школе. Одной из форм абстрактного мышления является «понятие». Очень важно, начиная с начальной школы грамотно формировать у учащихся геометрические понятия, то есть учить младших школьников выделять существенные признаки того или иного понятия, обучать использовать основные логические приёмы формирования понятия. А именно учить анализу, синтезу, сравнению, классификации.

Мы проанализировали учебно-методические комплексы авторов: Моро М.И.[14.4], Петерсон Л. Г., Истоминой Н.Б., Рудницкой В.Н.[15,5] В учебно-методическом комплексе Рудницкой В. Н.[15.5] в большей мере уделяется внимание заданиям для грамотного формирования геометрических понятий. В большинстве же учебно-методических комплексах на наш взгляд не достаточно заданий на грамотное и точное формирование геометрических понятий.

Противоречие состоит в том, что достаточное число разработок и исследований представлено, для учителей начальной школы в области геометрии, учителя, методисты говорят о внедрении большего объёма геометрии в начальный курс математики, а на практике оказывается всё по-другому.

Никто не будет спорить с тем, что каждый учитель должен развивать

логическое мышление учащихся. Об этом говорится в объяснительных

записках к учебным программам, об этом пишут в методической литературе

для учителей. В результате работа над развитием логического мышления

школьников идет «вообще» - без знания системы необходимых приемов.

Это приводит к тому, что боль­шинство учащихся не овладевают такими

приёмами, как анализ, синтез и классификация, даже в старших классах

школы, а эти приемы не­обходимы уже младшим школьникам: без них не

происходит полноценного усвоения материала.

Вопрос о том, каким должно быть обучение геометрии в начальной школе

В последнее время привлекает внимание многих исследователей, так например

И.Ф.Шарыгин[29,4c] разработал концепцию широкой геометритизации всего

Изучаемого математического материала с 1-го по 6-й классы. Шадрина в своём

учебном пособии об этом пишет и сама внесла большой вклад в

образование геометрии в начальных классах. [28,10c]

Противоречие возникает в том, что разработано множество методик, проведены

Исследования по данной теме, но учебно – методическое обеспечение по

математике для начальных классов и сами учителя не включают это в

программу.

Из всего выше сказанного, следует проблема: влияет ли развитие умения

использовать логические приёмына повышение качества формирования

понятия «многогранник» у четвероклассников.

Область нашего исследования: педагогика и психология начальной школы, методика преподавания математики.

Объект исследования: методика развития умения использовать логические приёмы

Предмет исследования: развитие умения использовать логические приёмы при формировании понятия «многогранник» у четвероклассников с использованием компьютера.

Цель исследования: доказать, что развитие умения использовать логические приёмы способствует повышению качества формирования понятия «многогранник» у четвероклассников.

Задачи:

1. Изучить и проанализировать учебно-методическую литературу по теме ВКР.

2. Дать анализ состояния проблемы в современной науке.

3. Провести наблюдение за группой учеников класса в процессе проведения исследования.

4. Разработать систему заданий по теме ВКР.

5. Экспериментально проверить эффективность использования логических приёмов при формировании понятия «многогранник».

Методы исследования:

• Наблюдение;

• Беседа;

• Изучение педагогического опыта;

• Диагностические задания;

• Анкетирование;

• Анализ детских работ;

• Эксперимент.

Глава I (теоретическая). Изучение понятия многогранник в начальных

классах.

1.1.Психологические особенности младшего школьного возраста.

Границы младшего школьного возраста, совпадающие с периодом обучения в начальной школе, устанавливаются в настоящее время с 6-7 до 9—10 лет. В этот период происходит дальнейшее физическое и психофизиологическое развитие ребенка, обеспечивающее возможность систематического обучения в школе.[19,182]

Начало обучения в школе ведет к коренному изменению социальной ситуации развития ребенка. Он становится «общественным» субъектом и имеет теперь социально значимые обязанности, выполнение которых получает общественную оценку. На протяжении младшего школьного возраста начинает складываться новый тип отношений с окружающими людьми. Безусловный авторитет взрослого постепенно утрачивается и к концу младшего школьного возраста все большее значение для ребенка начинают приобретать сверстники, возрастает роль детского сообщества

Ведущей в младшем школьном возрасте становится учебная деятельность. Она определяет важнейшие изменения, происходящие в развитии психики детей на данном возрастном этапе. В рамках учебной деятельности складываются психологические новообразования, характеризующие наиболее значимые достижения в развитии младших школьников и являющиеся фундаментом, обеспечивающим развитие на следующем возрастном этапе. Постепенно мотивация к учебной деятельности, столь сильная в первом классе, начинает снижаться. Это связано с падением интереса к учебе и с тем, что у ребенка уже есть завоеванная общественная позиция ему нечего достигать. Для того чтобы этого не происходило учебной деятельности необходимо придать новую лично значимую мотивацию. Ведущая роль учебной деятельности в процессе развития ребенка не исключает того, что младший школьник активно включен и в другие виды деятельности, в ходе которых совершенствуются и закрепляются его новые достижения.

Согласно Л.С. Выгодскому, с началом школьного обучения мышление выдвигается в центр сознательной деятельности ребенка. Развитие словесно-логического, рассуждающего мышления, происходящее в ходе усвоения научных знаний, перестраивает и все другие познавательные процессы: «память в этом возрасте становится мыслящей, а восприятие — думающим».[ 3, 198]

На протяжении младшего школьного возраста в развитии внимания происходят существенные изменения, идет интенсивное развитие всех его свойств: особенно резко (в 2,1 раза) увеличивается объем внимания, повышается его устойчивость, развиваются навыки переключения и распределения. К 9-10 годам дети становятся способны достаточно долго сохранять внимание и выполнять произвольно заданную программу действий.

В младшем школьном возрасте память, как и все другие психические процессы, претерпевает существенные изменения. Суть их состоит в том, что память ребенка постепенно приобретает черты произвольности, становясь сознательно регулируемой и опосредованной.

Такие психологи, как В. Д. Шадриков и Л.В. Черемошкина выделили 13 способов организации запоминаемого материала: группировка, выделение опорных пунктов, составление плана, классификация, структурирование, схематизация, установление аналогий, мнемотехнические приемы, перекодирование, достраивание запоминаемого материала, серийная организация ассоциации, повторение.[27,18]

Трудность выделения главного, существенного отчетливо проявляется в одном из основных видов учебной деятельности школьника — в пересказе текста. Психолог А.И. Липкина [13,54], исследовавшая особенности устного пересказа у младших школьников, заметила, что краткий пересказ дается детям гораздо труднее, чем подробный. Рассказать кратко — это значит выделить основное, отделить его от деталей, а именно этого дети не умеют.

В этом возрасте происходит появление и другого важного новообразования — произвольного поведения. Ребенок становится самостоятельным, сам выбирает, как ему поступать в определенных ситуациях

С формированием у младших школьников произвольного поведения тесно связаны такие новообразования, как планирование результатов действия и рефлексия.

Именно в этом возрасте ребенок переживает свою уникальность, он осознает себя личностью, стремится к совершенству. Это находит свое отражение во всех сферах жизни ребенка, в том числе и во взаимоотношениях со сверстниками. Дети находят новые групповые формы активности, занятий. Они стараются по началу вести себя так, как принято в этой группе, подчиняясь законам и правилам. Затем начинается стремление к лидерству, к превосходству среди сверстников. В этом возрасте дружеские отношения более интенсивные, но менее прочные. Дети учатся умению приобретать друзей и находить общий язык с разными детьми. Хотя предполагается, что способность к формированию близких дружеских отношений в некоторой степени определяется эмоциональными связями, установившимися у ребенка в течение первых пяти лет его жизни.

Таким образом, младший школьный возраст является наиболее ответственным этапом школьного детства.

Основные достижения этого возраста обусловлены ведущим характером учебной деятельности и являются во многом определяющими для последующих лет обучения: к концу младшего школьного возраста ребенок должен хотеть учиться, уметь учиться и верить в свои силы.

Интенсивное  развитие интеллекта происходит в младшем школьном возрасте.

Ребенок, особенно 7-8 летнего возраста, обычно мыслит конкретными категориями, опираясь при этом на наглядные свойства и качества конкретных предметов и явлений, поэтому в младшем школьном возрасте продолжает развиваться наглядно-действенное и наглядно-образное мышление, что предполагает активное включение в обучение моделей разного типа (предметные модели, схемы, таблицы, графики и т.п.)[10,52]

Учителя знают, что мышление у детей одного и того же возраста достаточно разное. Одни дети легче решают задачи практического характера, когда требуется использовать приемы наглядно-действенного мышления , например задачи, связанные с конструированием и изготовлением изделий на уроках труда. Другим легче даются задания, связанные с необходимостью воображать и  представлять какие-либо события или какие-нибудь состояния предметов или явлений. Например, при написании изложений, подготовке рассказа по картинке и т.п. Третья часть детей легче рассуждает, строит условные суждения и умозаключения, что позволяет им более успешно, чем остальным детям, решать математические задачи, выводить общие правила и использовать их в конкретных случаях.

Встречаются такие дети, которым трудно и  мыслить практически и оперировать образами, и рассуждать, и такие, которым все это делать легко.

Наличие такого разнообразия  в развитии разных видов мышления у разных детей в значительной мере затрудняет и осложняет работу учителя. Поэтому ему целесообразно более отчетливо представлять  основные уровни развития видов мышления у младших школьников.

О наличии того или иного вида мышления у ребенка можно судить по тому, как он решает соответствующие данному виду мышления  задачи. Так, если при решении легких задач – на практическое преобразование предметов, или на  оперирование их  образами, или на  рассуждение – ребенок  плохо  разбирается в их условии, путается  и теряется  при поиске их решения,  то в этом случае считается, что у него первый уровень развития в соответствующем виде мышления.

Если ребенок  успешно решает легкие задачи, предназначенные для применения того или иного вида мышления, но затрудняется в решении более сложных задач, в частности из-за того, что ему не удается представить все это решение целиком, поскольку недостаточно развито умение планировать,  то в этом случае считается, что  у него второй уровень развития в соответствующем виде мышления.

И наконец, если ребенок успешно решает и легкие и сложные задачи в рамках соответствующего вида мышления и даже может помочь другим  детям в решении легких задач, объясняя причины допускаемых ими ошибок, а так же  может  придумывать сам легкие задачи, то этом случае считается, что у него третий уровень развития соответствующего  вида мышления.

Опираясь на эти уровни в развитии мышления, учитель сможет более конкретно охарактеризовать мышление каждого ученика.

Для умственного развития младшего  школьника нужно использовать три вида  мышления. При этом с помощью каждого из них у ребенка  лучше  формируются те или иные качества  ума.  Так решение задач  с помощью наглядно-действенного мышления позволяет развить у учеников навыки управления своими действиями,  осуществление целенаправленных, а не случайных и хаотичных попыток  в решении задач.

Итак, существует три вида мышления: наглядно-действенное, наглядно-образное, словесно-логическое. Уровни мышления у детей одного и того же  возраста достаточно  разные. Поэтому задача педагогов, психологов состоит в дифференцированном подходе к  развитию мышления у младших школьников.[17,40]

1.2.Понятие, как форма абстрактного мышления.

Понятие является одной из форм абстрактного мышления. [4.13]

Свойства — это то, в чем предметы сходны друг с другом или отличные друг от друга. Свойства бывают существенные и несущественные.

Понятие — форма абстрактного мышления мышления, в которой отражаются существенные свойства одноэлементного класса или класса однородных предметов.

Всякое понятие имеет содержание и объем. Содержанием понятия называется совокупность существенных свойств одноэлементного класса или класса однородных предметов, отраженных в этом понятии. Содержанием понятия «ромб» является совокупность двух существенных свойств: «быть параллелограммом» и «иметь равные стороны».

Объемом понятия называют класс обобщаемых в нем предметов. Объективно, т.е. вне сознания человека, существуют различные предметы, например, прямоугольники. Под объемом понятия «прямоугольники» подразумевается множество всех прямоугольников, которые существуют сейчас, существовали ранее и будут существовать в будущем.

Понятия можно классифицировать по объему и по содержанию. По объему понятия делятся на единичные, общие и пустые.

Объем единичного понятия составляет одноэлементный класс (например, «модель многогранника пирамида сделанная Петей Васечкиным во втором классе» и др.).

Объем общего понятия включает число элементов больше единицы (например, «пирамида», «куб», «тетрайдэр» и др.).

Кроме общих и единичных понятий по объему выделяют понятия пустые (с нулевым объемом), т.е. такие, объем которых представляет пустое множество (например, «треугольная пирамида», «круглый квадрат», и др.)

По содержанию можно выделить следующие четыре пары понятий.

Конкретные и абстрактные понятия.

Конкретными называются понятия, в которых отражены одноэлементные или многоэлементные классы предметов (как материальные, так и идеальные).

Относительные и безотносительные понятия.

Относительные — такие понятия, в которых мыслятся предметы, существование одного из которых предполагает существование другого.

Безотносительные — такие понятия, в которых мыслятся предметы, существующие самостоятельно, вне зависимости от другого предмета («треугольник», «тетраэдр»).

Положительные и отрицательные понятия.

Положительные понятия характеризуют в предмете наличие того или иного качества или отклонения.

Отрицательными называют те понятия, которые означают, что указанное качество отсутствует в предметах

Собирательные и не собирательные понятия.

Собирательными называют понятия, в которых группа однородных предметов мыслится как единое целое (например, «множество», «натуральные числа»)

Определение понятия — это такая логическая операция, которая раскрывает содержание понятия либо устанавливает значение термина.

Реальные и номинальные определения

Если определяется понятие, то определение будет реальным. Если определяется термин, обозначающий понятие, то определение будет номинативным.

С помощью номинативных определений вводятся также новые термины, краткие имена взамен более сложных описаний предметов. Например, «навыком называется такое действие, в составе которого отдельные операции стали автоматизированными в результате упражнений».

Определения могут быть явными и неявными.

Явные определения.

Явные определения — это такие, в которых даны определяемое понятие и определяющее понятие, и между ними устанавливается некоторое отношение равенства, эквивалентности. Самое распространенное явное определение — определение через ближайший род и видовое отличие. В нем устанавливаются существенные признаки определяемого понятия. Например: «Правильный многоугольник — многоугольник, у которого все стороны конгруэнтны и все углы равны.

Признак, указывающий не тот круг предметов, из числа которых нужно выделить определяемое множество предметов, называется родовым признаком, или родом. В приведенных примерах родовыми являются понятия «многоугольник», «прибор».

Признаки, при помощи которых выделяется определяемое множество предметов из числа предметов, соответствующих родовому понятию, называются видовым отличием. При определении понятия видовых признаков (отличий) может быть один или несколько.

К явным определениям понятий относят и генетические определения. Они часто встречаются в школьных учебниках. Генетическими называются определения предмета путем указания на способ, которым образуется только данный предмет и никакой другой (это его видовое отличие). Например: «Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех попарно соединяющих их отрезков».

Неявные определения.

В отличии от явных определений, в неявных определениях на место определяющего понятия поставлен контекст или набор аксиом, или описание построения объекта, или показ.

1) В контекстуальных определениях содержание нового понятия раскрывается через отрывок текста, через контекст, через анализ конкретной ситуации, описывающий смысл вводимого понятия. Примером контекстуального определения может быть теорема и её доказательство.

В начальной школе при введении понятий чаще всего используются остенсивные и контекстуальные определения. Иногда встречаются определения, сочетающие контекст и показ. Примером такого определения является определение прямоугольника, приведенное в учебнике математики для II класса [18,22]. Здесь нарисованы (показаны) четырехугольники и приведен текст: «У этих четырехугольников все углы прямые». Под рисунком написано: «Это прямоугольники». Очень редко определения понятий даются через род и видовое отличие. Так, например, определяют умножение: «Сложение одинаковых слагаемых называется умножением».

Основными логическими приемами формирования понятий являются анализ, синтез, сравнение, абстрагирование, обобщение.

Для выделения существенных признаков необходимо абстрагироваться (отвлечься) от несущественных, которых в любом предмете очень много. Этому служит сравнение, сопоставление предметов. Для выделения ряда признаков следует произвести анализ, т.е. мысленно расчленить целый предмет на его составные части, элементы, стороны, отдельные признаки, а затем осуществить обратную операцию — синтез (мысленное объединение частей предмета, отдельных признаков, притом признаков существенных, в единое целое.

Мысленному анализу как приему, используемому при образовании понятий, часто предшествует анализ практический, т.е. разложение, расчленение предмета на его составные части. Мысленному синтезу предшествует практический сбор частей предмета в единое целое, с учетом правильного взаимного расположения частей при сборке.

Анализ — мысленное расчленение предметов на их составные части, мысленное выделение в них признаков.[6,10]

Синтез — Мысленное установление сходства или различия предметов по существенным или несущественным признакам.[6,16]

Абстрагирование — мысленное выделение одних признаков предмета и отвлечение от других. Часто задача состоит в выделении существенных признаков и в отвлечении от несущественных, второстепенных.[6,20]

Обобщение — мысленное объединение отдельных предметов в некотором понятии.[6,24]

Перечисленные выше логические приемы используются при формировании новых понятий как в научной деятельности, так и при овладении знаниями в процессе обучения.[4,62]

1.3.Геометрическое определение понятия « многогранник».

Математик В.А. Тиморин дал следующие определения многогранникам [24,10]:

Многогранником называется тело, граница которого является объединением конечного числа многоугольников.

Многогранник — поверхность, составленная из многоугольников, а также тело ограниченное такой поверхностью.

Многоугольник — это геометрическая фигура, определяется как замкнутая ломаная.

Вершины ломаной называются вершинами многоугольника, а отрезки — сторонами многоугольника.

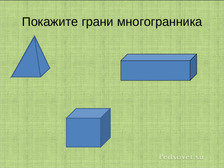
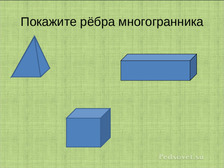
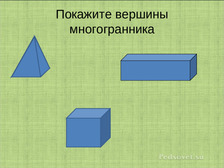
Эти многоугольники называются гранями, их стороны — рёбрами, а их вершины — вершинами многогранника.

Первые упоминания о многогранниках известны еще за три тысячи лет до нашей эры в Египте и Вавилоне. Но теория многогранников является и современным разделом математики. Она тесно связана с топологией, теорией графов, имеет большое значение как для теоретических исследований по геометрии, так и для практических приложений в других разделах математики, например, в алгебре, теории чисел, прикладной математики - линейном программировании, теории оптимального управления.

Многогранники имеют красивые формы, например, правильные, полуправильные и звездчатые многогранники. Они обладают богатой историей, которая связана с именами таких ученых, как Пифагор, Евклид, Архимед.

Среди всех простых многогранников ещё в древности были обнаружены такие, у которых все грани правильные и равные между собой многоугольники, то есть такие число сторон которых одно и то же, и все стороны каждого многоугольника равны [28,38].

Многогранник называется выпуклым, если весь он лежит по одну сторону от плоскости любой его грани [28,38]. Выпуклый многогранник, называется правильным, если:

1. Все его грани – правильные многоугольники;

2. Все грани многогранника равны.

История правильных многогранников уходит в глубокую древность. Правильными многогранниками занимались Пифагор и его ученики. С тех пор правильные многогранники стали называться Платоновыми телами.

Существует несколько видов многогранников: тетраэдр, гексаэдр (куб), октаэдр, додекаэдр, икосаэдр. Почему правильные многогранники получили такие имена? Это связано с числом их граней. Тетраэдр имеет 4 грани, в переводе с греческого "тетра" - четыре, "эдрон" - грань. гексаэдр (куб) имеет 6 граней, "гекса" - шесть; октаэдр - восьмигранник, "окто" - восемь; додекаэдр - двенадцатигранник, "додека" - двенадцать; икосаэдр имеет 20 граней, "икоси" - двадцать.

Кроме полуправильных многогранников из правильных многогранников - Платоновых тел, можно получить так называемые правильные звездчатые многогранники. Их всего четыре, они называются также телами Кеплера - Пуансо. (Приложение 1) Кеплер открыл малый додекаэдр, названный им колючим или ежом, и большой додекаэдр. Пуансо открыл два других правильных звездчатых многогранника, двойственных соответственно первым двум: большой звездчатый додекаэдр и большой икосаэдр.

1.4. Обучение геометрии в начальных классах.

Цели обучения геометрии в начальной школе не могут быть сформулированы в отрыве от целей школьного обучения как такового. В самом общем виде эти цели на современном этапе развития школьного образования в России могут быть обозначены следующей парадигмой: центром всего учебно-воспитательного процесса является конкретный ученик во всем многообразии его индивидуальных черт. Отсюда следует, что основной целью школьного образования является обеспечение каждому учащемуся полноценного личностного развития в максимально возможном диапазоне его психологических ресурсов.

Первая цель обучения геометрии в начальной школе: создание для каждого ученика психологически комфортной познавательной среды.

Еще одна цель обучения геометрии младших школьников: развитие пространственного мышления учащихся.

Третья цель обучения геометрии в начальной школе: развитие образного мышления как средства создания условий для усвоения детьми содержательного смысла математических понятий.

Формирование представлений о многогранниках следует начать со сравнений поверхностей тетраэдра, куба. Дети выделяют их общие свойства: все эти поверхности замкнутые, каждая склеенная из кусков, а так же те свойства, которыми они различаются. Различаются они и количеством кусков. Берем в руки модель тетраэдра и начинаем путешествие по его поверхности; проходим по ней, показывая свое местонахождения обратной стороной карандаша. Замечаем, что можно обойти всю его поверхность, двигаясь от одного плоского куска к другому, переходя через места склейки, которые представляют собой отрезки, а в концах этих отрезков встречаются сразу три отрезка. Ту же самую работу проводим с моделью куба. Вводим термины: обе поверхности – многогранники: места склейки плоских кусков - ребра многогранника; места встречи нескольких ребер – вершины многогранника; плоские куски поверхности – грани многогранника.

Затем рассматриваем изображение многогранников на рисунке. Подсчитываем количество граней, ребер, вершин у каждого из изображенных многогранников. Сравнение изображений пирамид и призм приводит выделению их различий: у одних многогранников все грани, кроме одной, сходятся в одной вершине, а у других, такой вершины нет.

Знакомим детей с названием многогранников по числу граней: четырехгранники, шестигранники и другие.

Представление учащихся о многоугольнике формируется как участие поверхности многогранника – граням многогранника.

Работа по изучению геометрического материала должна проводится как в естественнонаучной дисциплине: свойства фигур выявляются экспериментально, усваиваются необходимая терминология и навыки. Поэтому важное место в обучении должен занимать лабораторный метод.

Общаясь с разнообразными материальными моделями геометрических фигур, выполняя с этими моделями большое число опытов, учащиеся выясняют наиболее общие признаки, не зависящие от материала, цвета, положения, веса и т.п.

Это достигается систематическим применением приема материализации изучаемых геометрических объектов. Например, перпендикулярные прямые – это не только объект, полученный с помощью линейки и карандаша, но и края парты, классная доска, пол, потолок, оконная рама, клеточки тетради и многое другое. Отвлекаясь от конкретных свойств материальных вещей, учащиеся овладевают геометрическими представлениями.

Значительное место в разработанной методике занимает применение приема сопоставления и противопоставления геометрических фигур. Это позволяет уточнить свойства фигур, их классификацию. Например, выделение множества треугольников из множества многоугольников, выделение квадратов из множества прямоугольников.

Как показало исследование, созданный запас геометрических представлений обеспечивает необходимую основу для проведения в дальнейшем работы по формированию геометрических понятий.

Отличительной чертой преподавания начальной геометрии в наше время от прошлых лет является существование параллельных систем развивающего обучения, новых учебников и учебных комплексов, позволяет создать учителям начальных классов условия для формирования своих содержательных моделей начального образования путем самостоятельного составления учебного плана и набора к нему учебных курсов.

Имея такое право, отмеченное в законе РФ об образовании в ст. 55 п. 4 «При исполнении профессиональных обязанностей преподаватели имеют право на свободу выбора в использовании методик обучения и воспитания, учебных пособий и материалов, учебников, методов оценки знаний обучающихся, воспитанников» [9,с53], учитель, чтобы им пользоваться, должен быть уверен в своих действиях. Он должен учить, наверняка зная, что предложенный им вариант обучения даст положительные результаты, для чего учителю необходимы не только теоретические знания преподаваемого предмета, курса, но и знания тех исследований, которые проводились и ведутся в области его интересов.

Поэтому, чтобы решить задачи нашего исследования в плане геометрической подготовки учащихся начальных классов, мы обратились к наиболее интересным исследованиям прошлого и сегодняшнего дня, посвященным изучению геометрического материала в начальных классах, чтобы знать чему можно учить младших школьников.

Такими исследованиями занимались методисты-математики М.В. Богданович [16 ,с2], С.И. Волкова [14,с10], Н.Н. Столярова [2,с22], В.В. Давыдов [7,с 2] и др.

В исследованиях, посвященных обучению элементам геометрии в начальных классах, подтверждается возможность и необходимость введения начального курса геометрии в значительно расширенном объеме изучения геометрического материала, чем это предусматривается отдельными из ныне действующих программ. Проанализировав программу по математике Э.И. Александровой (система развивающего обучения Эльконина-Давыдова) мы пришли к выводу, что в ее содержании не предусматривается знакомство учащихся с теми геометрическими понятиями и объектами, которые составляют основу изучения величин и действий над ними.

Кроме того, обучение начальному курсу геометрии играет важную роль в развитии пространственного и логического мышления учащихся младших классов, в усвоении и накоплении знаний по основным геометрическим понятиям, готовит учащихся к активному и осмысленному восприятию систематического курса геометрии в средних и старших классах школы, ведь геометрический материал является одним из основных элементов всякого математического образования.

1.4.1.Анализ учебно-методических комплексов.

Нами были проанализированы учебно-методические комплексы: Моро М.И., Петерсон Л. Г., Истоминой Н.Б., Рудницкой В.Н.

В учебно-методическом комплексе Моро М.И. представлено довольно мало геометрического материала, в большей мере геометрический материал тут представлен как дополнительный материал для самостоятельного изучения. Программа направлена на формирование устойчивых навыков устных и письменных вычислений. Этому способствует хорошо распределенная во времени, оптимально насыщенная система упражнений, направленных на усвоение отношений между единицами измерения величин и действий с величинами.

В учебно-методическом комплексе Петерсон Л.Г. геометрического материала представлено больше чем у Моро М.И., Но материал дан без какой-либо чёткой последовательности. Программа преследует цели обновления содержания и методов обучения математике с позиций комплексного развития личности, гуманизации, гуманитаризации и экологизации образования. Одна из основных задач - обучение построению, исследованию и применению математических моделей окружающего мира.

В учебно-методическом комплексе Истоминой Н.Б. присутствует геометрический материал в малом объёме, прослеживается определённая закономерность (от простого к сложному). Программа направлена на целенаправленное и непрерывное формирование приемов умственной деятельности (анализа, синтеза, сравнения, классификации, проведения аналогий и обобщений) в процессе математического образования. Существенно изменена традиционная последовательность изучения материала. Использование логических приёмов при обучении не сомненый плюс программы, но не хватает геометрического материала. У Истоминой Н.Б. почти не идёт речь о «многогранниках» и «многоугольниках» их не сравнивают между собой.

В учебно-методическом комплексе Рудницкой В. Н. в большей мере уделяется внимание заданиям для грамотного формирования геометрических понятий. В большинстве же учебно-методических комплексах на наш взгляд не хватает заданий на грамотное и точное формирование геометрических понятий. В программе Рудницкой представлены, как «многоугольники», так и «многогранники». Этим геометрическим телам не даётся явное определение, но учащиеся имеют о них представление.

Отсюда возникает противоречие: можно ли использовать разработанную нами систему упражнений для развития в большей степени абстрактного мышления у учащихся, учить логическим приёмам мышления.

Глава II (практическая) Развитие умения использовать логические приёмы при формировании понятия «многогранник» у четвероклассников с использованием компьютера.

2.1.Выявление уровня знаний о понятиях «многогранник» у учеников 4-х классов (констатирующий этап).

Цель: выявить уровень развития умения использовать логические приёмы при формировании понятий «многогранник».

Исследования проводились во время прохождения практики в школе №1287.

Ученики занимались по учебно-методическому комплексу Рудницкой В.Н.

К моменту проведения исследования ученики, обучаясь по данной программе, должны были обладать следующими знаниями: Знать названия многих многогранников, элементы многогранников, внешний вид многогранников. Основываясь на этих знаниях, нами было проведено первое анкетирование на констатирующем этапе.

2.1.1.Краткая характеристика учеников группы.

Для исследования была взята группа из 10 учеников 4 класса А.

У одного из учеников (Рома Р.) по математике была отметка 3(удвл.). У шестерых учеников ( Борис К., Дмитрий Л., Евгения А., Евгений Г., Игорь Г., Николай П.) была отметка 4 (хор.). Три ученика (Виктория Х., Жанна Х., Стёпа К.) по математике имели отметку 5 (отл.)

Все ученики кроме Ромы Р. Называли одним из своих любимых предметов математику. Виктория Х. и Жанна Х. регулярно посещали факультатив, по логике начиная с 1-го класса. Стёпа К., Игорь Г., Дмитрий Л. cказали о том, что любят больше геометрический материал в уроке математики.

У каждого ученика уже в четвёртом классе есть своё хобби, увлечение.

2.1.2 Проведение анкетирования.

В Анкете использовались следующие вопросы:

1. Перечислите знакомые вам многоугольники.

2. Перечислите знакомые вам многогранники.

3. Начертите многоугольник.

4. Начертите многогранник.

5. Знаете ли вы, что такое развёртка многогранника?

6. Встречались ли вы когда-нибудь с развёрткой многогранников в повседневной жизни?

7. Перечислите название многогранников, которые вы чаще всего встречаете в повседневной жизни.

8. Какие многогранники вы встречаете чаще всего в повседневной жизни.

9. Подчеркните слова, которые обозначают многоугольники прямой линией, а слова, которые обозначают многогранники волнистой линией: Круг, треугольник, прямоугольник, куб, пирамида, параллелепипед, пятиугольник, тетраэдр, шестиугольник.

10. Отметьте галочкой знакомые вам многогранники.

11. Подпишите знакомые вам названия многогранников.

Для проведения исследования использовались анкета (приложение 2).

В приложении «2» представлены результаты проведённого анкетирования.

Проведение анкетирования:

Детям предлагалась анкета с инструкциями, и достаточное количество времени (10 минут). За каждый положительный ответ ребёнок получал 1 балл, за ответ нет, не знаю или его отсутствие ребёнок получал 0 баллов. Таким образом, при всех положительных ответах ребёнок получал 11 баллов. И соответственно если были все отрицательные ответы, то ребёнок получал 0 баллов.

Инструкции к проведению анкетирования:

Заполнить анкету. На вопросы: 6, 7, 8 ответить да или нет. На все остальные вопросы анкеты отвечать, полным ответом. Задания 9,10,11 выполнять соответственно заданию.

Инструкции к выполнению анкеты были представлены ученикам, как в устной форме, так и на доске.

Дополнительных вопросов во время проведения анкетирования у учеников не возникло.

Результаты ученикам не сообщались.

2.1.3Анализ анкетирования.

Были выделены три уровня знаний о понятиях многогранник и многоугольник у учащихся 4-х классов:

Высокий;

Средний;

Низкий.

Высокий уровень	Средний уровень	Низкий уровень
Ребёнок справился с работой раньше отведенного срока.	Ребёнок выполнил задания в срок.	Ребёнок не справился за отведённое время с работой.
На 8-11 заданий были выполнены верно.	4-7 заданий было верно выполненно	Не выполнил задания либо справился с 3 и менее заданиями.

Таким образом, 8-11 баллов - Высокий уровень

4-7 баллов – Средний уровень

0-3 балла – Низкий уровень

Для анализа некоторых характеристик мыслительного процесса, учитывалось время, затраченное на ответ. Это характеризовало уровень его импульсивности. Как правило, импульсивные дети, стремящиеся к быстрым, часто необдуманным действиям, подвижные, иногда даже расторможенные, затрачивают на данное в задание не более 10 минут. Как правило, они стремятся быстрее закончить работу, избавиться от неё, поэтому набирают небольшое количество баллов. Такие дети плохо ориентируются в задании, им не хватает терпения и усидчивости.

Ответы на вопросы зачастую, были положительными, но не полными.

Многоугольник смогли изобразить многие ученики. С изображением многогранников у большинства учеников возникли затруднения.

На 6-7 вопросы анкеты ученики все затруднялись ответить, так как никто из них не сталкивался никогда с развёрткой каких-либо геометрических фигур.

Так же выяснилось, что ученики никогда прежде не обращали внимание на, то что их окружают многогранники в повседневной жизни.

На основе характеристик представленных в таблице дети были распределены по уровням.

Полученные данные были подвергнуты обработке, в результате чего было составлена линейная диаграмма.

Из Диаграммы видно, что большинство учеников относится к группе со средним уровнем развития(70%), к группе учеников с низким уровнем развития относятся 10%, и к крупе учеников с высоким уровнем относится лишь 20% учеников.

Учащихся с низким уровнем: 10%

Учащихся со средним уровнем: 70%

Учащихся с высоким уровнем: 20%

После проведения анкетирования, несколько учеников обратилось с просьбой помочь им объяснить, рассказать ответы на данные вопросы.

2.1.4Вывод.

На основе полученных результатов констатирующего исследования появилась необходимость систематически включать в процесс изучения математики больше геометрии. Использовать различные логические приёмы при формировании понятий «многогранник».

Никто не будет спорить с тем, что каждый учитель должен развивать логическое мышление учащихся. Об этом говорится в объяснительных записках к учебным программам, об этом пишут в методической литературе для учителей. Однако кон­кретной программы логических приемов мышления, которые должны быть сформированы при изучении данного предмета, пока нет. В результате работа над развитием логического мышления школьников идет «вообще» - без знания системы необходимых приемов, без знания их содержания и последо­вательности формирования. Это приводит к тому, что боль­шинство учащихся не овладевают начальными приемами мышления даже в старших классах школы, а эти приемы не­обходимы уже младшим школьникам: без них не происходит полноценного усвоения материала.

Мы рассчитываем, что разработанная нами методика поможет ученикам с низким и средним уровнем знаний по данной теме повысить свой уровень знаний, а ученикам с высоким уровнем знаний по данной теме закрепить свои знания.

У учеников нет системности при изучении данной темы. Ученики никогда не сравнивали многогранники с многоугольниками. Очень часто путают их между собой, путаются в названиях этих фигур.

Оказалось, что только небольшая часть учащихся владеет логическими приемами хорошо, у остальных они не сформированы в должной мере. Больше того, у многих учащихся начальной школы не сформированы и более элементарные логические операции.

Причина ошибок состоит в неумении ученика дифференцировать отдельные стороны предметов, в результате чего изменение одного свойства (формы фигуры) он принимает за изменение другого (площади фигуры), которое в данном случае оставалось неизменным. В старших классах подобные логические ошибки исчеза­ют, но, к сожалению, сохраняются многие другие. Так, на­пример, простейшие задачи на распознавание объектов, относящихся к понятиям с дизъюнктивной структурой при­знаков (или - или), вызывают затруднения у учащихся вплоть до окончания школы.

Ученики не использовали, ни каких логических операций. Многие ученики никогда не оборачивались вокруг себя и не замечали, что кругом они встречают многогранники. Не задумывались о геометрии в повседневной жизни.

2.2.Формирующий этап.

Цель: повысить уровень развития умения использовать логические приёмы (анализ, синтез, классификация и др.) при формировании понятий «многогранник» у четвероклассников.

С учётом анализа учебно-методических комплексов была подобрана и разработана методика работы над понятиями «многогранник».

Естественно, что с любого логического приема работу на­чинать нельзя, так как внутри системы логических приемов мышления существует строго определенная последователь­ность, один прием строится на другом.

Вернемся к приему подведения под понятие и посмотрим, можно ли начинать формирование логических приемов мыш­ления с него. Для того чтобы решать вопрос о принадлежно­сти предмета к данному понятию, надо установить наличие у этого предмета системы необходимых и достаточных призна­ков. А это означает, что ученики к этому времени уже должны быть знакомы с понятиями необходимый признак и признак достаточный. Но эти понятия, в свою очередь, опираются на понятие существенный признак. Следовательно, учащиеся должны уметь дифференцировать признаки на существенные и несущественные. Последние, наконец, предполагают владе­ние понятием признак, свойство и умением выделять в предме­тах различные свойства. Как видим, усвоение приема подведения под понятие предполагает усвоение целой системы дру­гих логических знаний и операций: необходимых и достаточ­ных свойств, понимание того, чем отличается необходимое свойство от достаточного, что такое вообще свойства, как их выделять в предмете, чем отличается свойство существенное от свойства несущественного и др.

Значит, нельзя начинать формирование логического мыш­ления с приема подведения под понятие.

С чего же начинать?

Первое, чему необходимо научить учащегося, - это уме­нию выделять в предметах свойства. Дети первого класса обычно выделяют в предмете всего два-три свойства, в то время как в каждом предмете бесконечное множество различ­ных свойств. Так, если покажете детям карандаш и спросите:

«Что о нем можно сказать, какой он?», - ученики ответят, что он красный (или назовут какой-то другой цвет), круглый (если он имеет цилиндрическую форму), - и все. Больше, чем два-три свойства, они не могут выделить. Поэтому необхо­димо специально обучать детей умению видеть в предмете множество свойств. Для этого полезно показать им прием по выделению свойств в предметах - прием сопоставления дан­ного предмета с другими предметами, обладающими другими свойствами.

Заранее подбирая для сравнения различные пред­меты и последовательно сопоставляя с ними исходный, можно постепенно научить детей видеть в предметах множество та­ких свойств, которые ранее были от них скрыты.

Как только дети научатся выделять в предметах множество различных свойств, можно переходить к следующему компо­ненту логического мышления - формированию понятия об общих и отличительных признаках предметов.

После того как учащиеся научатся выделять в предметах общие и отличительные свойства, можно сделать следующий шаг - научить детей отличать в предметах существенные (важные) свойства, с точки зрения определенного понятия, от свойств несущественных (неважных), второстепенных.

Анализ учебников и программ показывает, что действие сравнения необходимо учащимся уже в первом классе. Вместе с тем если его не сделать предметом специального усвоения, то оно оказывается не усвоенным большинством школьников до конца учебного года.

2.2.1.Описание первого занятия (приложение 3).

Цель: Обобщить у учеников имеющиеся знания. Формировать общие представления о «многогранниках».

На первом занятии с учениками им были даны определения данных понятий. Понятие многоугольник было разобрано при помощи геометрического понятия угол.

Понятие многогранник было разобрано, при помощи понятия многоугольник.

• Многоугольник- это геометрическая фигура, имеющая 3 и более углов.

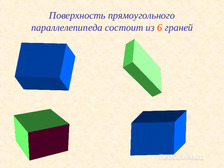
• Многогранник – это тело, граница которого состоит из многоугольников.

• Эти многоугольники называются гранями, их стороны — рёбрами, а их вершины — вершинами многогранника.

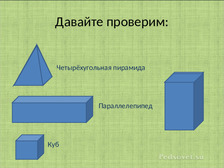
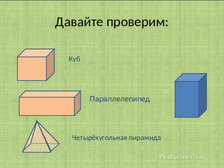
На первом занятии были рассмотрены несколько видов многоугольников: треугольник, квадрат, прямоугольник, пятиугольник, шестиугольник. Так же были рассмотрены многогранники основанием, которых служат раннее рассмотренные многоугольники. Например: куб, треугольная пирамида, четырёхугольная пирамида, параллелепипед.

Ученики на моделях сами показывали, какой многоугольник лежит в основании многогранника. Затем они доказывали это.

Находили на моделях грани, рёбра, вершины многогранников.

Большая часть занятия была уделена работе с чертежами многоугольников и работе с моделями многогранников.

Была проведена работа по парам: были розданы модели многогранников и дано задание – цветным карандашом или фломастером выделить на нём грани, рёбра и вершины.

Так же ученикам были представлены изображения многогранников, с которыми они раньше не встречались, такие как, малый и большой додекаэдр.

Во время проведения этого занятия ученики анализировали, синтезировали полученную информацию и классифицировали фигуры. Конечно же фигуры так же сравнивались между собой. Таким образом ученики уже на первом занятии использовали довольно большое количество логических приёмов.

2.2.2. Описание второго занятия (приложение 4).

Цель: Формирование представлений о прямоугольном параллелепипеде.

В начале второго занятия повторили пройденный материал на первом занятии.

На втором занятие было отдельно уделено внимание прямоугольному параллелепипеду.

Было дано определение данного понятия.

Была создана презентация (приложение 7). Говорили о том, где этот объект можно встретить в обычной жизни. Например: кирпич, холодильник и т.д.

Вспомнили, что такое грани и рёбра, вершины.

Изучили где у прямоугольного параллелепипеда грани, рёбра, вершины.

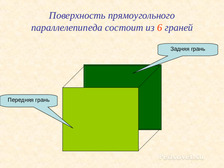
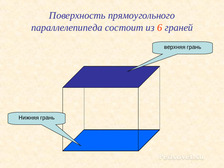
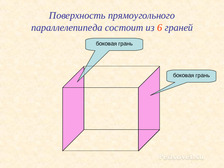
Разбирали, где находятся верхняя и нижняя грани, где находятся боковые грани, и где находятся задняя и передняя грани.

Ученикам было дано задание: Придумать, где в жизни мы встречаем другие многогранники.

Ответы были получены очень разные и интересные. Конечно, вспомнили про египетские пирамиды. Многие говорили о подставках для карандашей, о бытовых приборах, люстрах и т.д.

Один ученик вспомнил, что дома у него угловой шкаф, основанием которого является пятиугольник.

Оказалось, что многие ученики зачастую просто, не обращали внимание, что их окружает такое большое количество разнообразных многогранников.

Ученики под руководством и с использованием инструкций тренировались строить прямоугольный параллелепипед.

Во время этого занятия ученики так же анализировали, сравнивали многогранники с многоугольниками и классифицировали по различным принципам. И на этом занятии, несомненно, использовались логические приёмы мышления.

2.2.3.Описание третьего занятия (приложение 5).

Цель: Формировать представление о развёртке многогранников (практическое занятие).

На третьем занятие с учениками сначала было проведено повторение ранее изученного материала.

Использовался раздаточный материал: развёртка куба, клей.

В качестве наглядного материала был представлен видеофильм (приложение 8).

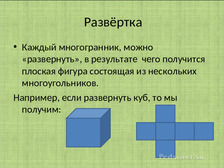
Каждый многогранник, можно «развернуть», в результате чего получится плоская фигура, состоящая из нескольких многоугольников.

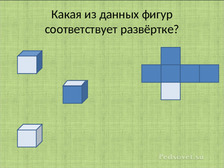
Ученикам было предложено самостоятельно склеить куб. Увидеть развёртку данной фигуры. Убедиться, что в основе такого многогранника как куб, действительно лежит квадрат, который является в свою очередь многоугольником.

Например, если развернуть куб, то мы получим:

Была составлена презентация (приложение 9) по средствам которой, ученики работали с различными видами развёрток.

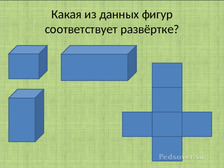
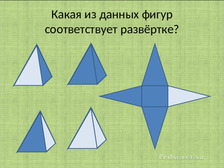
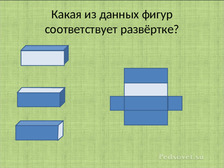
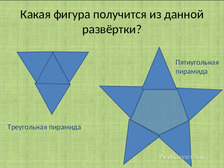
В презентации были представлены такие задания: Какая из предложенных фигур соответствует данной развёртке? Какая развёртка соответствует данной фигуре? Какая фигура получится из данной развёртки.

Использовались разные многогранники. Заштриховывались разные грани этих многогранников, для усложнения заданий.

Домой детям было дано задание: составить развёртку к шестиугольной пирамиде.

Ученики во время практического занятия были очень активны. У всех учеников это занятие вызвало положительные эмоции. Все ученики домой унесли модель куба, что не могло не вызвать положительных эмоций.

Ученики снова анализировали и синтезировали во время занятия.

2.2.4. Описание четвёртого занятия (приложение 6).

Цель: Закрепление пройденного материала.

4-е занятие было заключительным.

Не смотря на то что задание в конце прошлого занятия было добровольным все ученики принесли развёртку шестиугольной пирамиды. В начале была проведена проверка построения развёртки к шестиугольной пирамиде (приложение 9).

После чего было проведено общее повторение, в процессе которого говорили в основном сами ученики. Задавали вопросы если, что-либо было не понятно из всего ранее изученного материала.

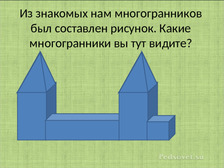
В виде презентации (приложение 9) были даны несколько заданий на повторение. Например: Из знакомых нам многогранников был составлен рисунок. Какие многогранники вы тут видите?

После выявления знакомых многогранников, обсуждали их, находили грани, рёбра, вершины. Говорили, о том какая фигура лежит в основании.

Во время всех занятий проводилась дополнительная работа с учениками в среде использования логических приёмов. Учащиеся постоянно сравнивали предметы («многогранники»), выявляли, что их объединяет, сравнивали, анализировали, классифицировали.

Ученики признались, что те, кто ходят на факультатив логики были знакомы с данными логическими операциями, но не умели их применять. Остальные ученики слышат об этом впервые и очень жалеют, что не использовали логически операции ранее. Некоторые ученики признаются, что использовали логические операции раньше, но не осознанно и не знали их названий.

2.5Вывод:

Детям была интересна данная тема. Даже те дети, у которых был высокий уровень знаний по данной теме узнали много нового. Особенно детей интересовали творческие задания. Придумать, склеить.

Так же интерес вызвала работа с моделями, так как каждый ученик мог потрогать, покрутить в руках, рассмотреть модели многогранников. После работы с моделями, каждый ученик точно понял, как выглядит многогранник и где у него находятся грани, рёбра и вершины. Далее любой из учеников группы с лёгкостью мог показать уже на любом многограннике, где находятся его грани, рёбра и вершины.

На вопрос что вы узнали нового, ученики говорили о том, что не знали, что тип многогранника можно определить по его основанию. Дети не знали о том, что в основе каждого, любого многогранника лежит многоугольник. После же проведённых занятий дети это усвоили и с лёгкостью могли отличить многогранник от других геометрических тел.

Так же вызвало интерес задание о том, что нас кругом окружают многогранники. Рома Р., например, рассказал о том, что теперь, когда идёт гулять часто ищет вокруг себя многогранники. Все согласились с ним и сказали, что делают так же, но не только на прогулке, но и дома, и в гостях, и в магазине, когда идут с родителями за покупками.

В процессе работы ученики постоянно анализировали, сравнивали и находили отличия, классифицировали предметы (многогранники), что способствовало их восприятию и пониманию данной темы. Во время занятий приходилось отступать от основной темы занятия и говорить с детьми о логических приёмах, о том какой целесообразнее использовать в данном задании. Что способствовало лучшему усвоению и понятию темы. Это не отвлекало, а наоборот заинтересовало учеников. Ученики запомнили, какие логические операции мы проводили, и будут использовать их как на других занятиях, так и в повседневной жизни.

Мы рассмотрели два логических приема: прием сравнения предметов, который дает возможность выделять множество свойств в предметах, и прием изменения свойств, который позволяет отличать свойства существенные от свойств несу­щественных. Прежде всего, вернемся к приему сравнения. Когда мы предлагали использовать этот прием для выделения учащими­ся различных свойств в предметах, то указывали, что предме­ты для сравнения должны подбираться учителем, никаких специальных требований к сравнению не предъявляли.

После знакомства учеников с различными видами свойств предме­тов прием сравнения можно формировать уже на более высо­ком уровне. Если этого не сделать, то у многих школьников он останется на житейском уровне: без осознания содержания этого приема и без умения произвольно и обоснованно ис­пользовать его как полноценное познавательное средство.

2.3. Выявление уровня знаний о понятиях многогранник и многоугольник у учеников 4-х классов (контрольный этап).

Цель: выявить уровень развития умения использовать логические приёмы при формировании понятий «многогранник».

2.3.1 Проведение анкетирования на контрольном этапе.

На контрольном этапе необходимо провести анкетирование, которое проводилось на констатирующем этапе. Для выявления уровня развития умения использовать логические приёмы при формировании понятий «многогранник» использовалась та же методика, что и на первом этапе нашего исследования, то есть анкетирование.

Ученикам была предложена анкета, на заполнение которой давалось 10 минут. Условия заполнения и критерии оценивания оставались прежними:

Инструкции к проведению анкетирования:

Заполнить анкету. На вопросы: 6, 7, 8 ответить да или нет. На все остальные вопросы анкеты отвечать, полным ответом. Задания 9,10,11 выполнять соответственно заданию.

Анкета (приложение 10):

1. Перечислите знакомые вам многоугольники.

2. Перечислите знакомые вам многогранники.

3. Есть ли что-то схожее между многогранником и многоугольником?

4. Начертите многоугольник.

5. Начертите многогранник.

6. Знаете ли вы, что такое развёртка многогранника?

7. Встречались ли вы когда-нибудь с развёрткой многогранников в повседневной жизни?

8. Видите ли вы вокруг себя многогранники в повседневной жизни.

9. Какие многогранники вы встречаете чаще всего в повседневной жизни.

10. Подчеркните слова, которые обозначают многоугольники прямой линией, а слова, которые обозначают многогранники волнистой линией:

Круг, треугольник, прямоугольник, куб, пирамида, параллелепипед, пятиугольник, тетраэдр, шестиугольник.

К ритерии оценивания работ были такими же, как и на констатирующем этапе: при правильном выполнение задания ученик получал 1 балл, при не верном ответе 0 баллов. Таким образом, при всех правильных ответах ученик получает 11 баллов.

Были выделены три уровня знаний о понятиях многогранник и многоугольник у учащихся 4-х классов:

8-11 баллов - Высокий уровень

4-7 баллов – Средний уровень

0-3 балла – Низкий уровень

Полученные данные контрольного этапа эксперимента были подвергнуты обработке.

Таким образом, на диаграмме видно, что после проведённой нами работы учеников с низким уровнем всего 10%, со средним уровнем 30%, и с высоким уровнем развития умения использовать логические операции 60%.

2.3.2.Вывод:

Таким образом, видно, что после проведённой нами работы учеников с низким уровнем всего 10%, со средним уровнем 30%, и с высоким уровнем развития умения использовать логические операции 60%.

Показания по сравнению с констатирующим этапом изменились в лучшую сторону. Ученики дают более точные и полные ответы, используя при этом различные логические операции.

Контрольный этап выявил, что проведенная и разработанная нами методическая работа, действительно помогает ученикам в развитие умения использовать различные логические приёмы при формировании таких понятий, как многогранник. При сравнении результатов констатирующего и контрольного этапов, сразу видно, что данная работа пошла на пользу. Ученики используют логические приемы и по отношению к другим предметам, и в повседневной жизни.

Все ученики с заданием анкеты контрольного этапа справились намного быстрее, чем с заданием анкеты констатирующего этапа. У очень малого количества учеников(всего 10 %) остался низкий уровень развития умения использовать логические приёмы при формирование понятий «многоугольник» и «многогранник». У большей части группы исследуемых детей уровень умения использовать логические приёмы поднялся с среднего до высокого. Контрольный этап проводился с целью выявить эту разницу. В связи с этим нами была составлена ещё одна диаграмма – сравнительная. В этой диаграмме очень чётко и хорошо видны различия.

Из диаграммы видно, что учеников с низким уровнем осталось столько же 10%, понизилось количество учеников со средним уровнем, но зато повысилось количество учеников с высоким уровнем. Из этого следует, что разработанные нами система заданий и проведённая работа действительно помогают ученикам.

2.4.Анализ проведённых исследований.

Мы ставили перед собой проблему: можно ли использовать разработанную нами систему упражнений для развития в большей степени абстрактного мышления у учащихся, учить логическим приёмам.

Проведённое нами исследование показало и доказало, что разработанную нами систему упражнений можно и нужно применять на практике.

Проблема решена положительно, так как исследования показали, что у группы учеников значительно повысился уровень умения использовать логические приёмы при формировании понятия «многогранник».

Сравнивая, результаты анкетирования на констатирующем этапе и на контрольном этапе мы можем сделать вывод, что разработанная нами система заданий помогла ученикам в развитии умений использовать логические операции при формировании понятия «многогранник» у четвероклассников.

В связи с тем, что наша проблема решена положительно, мы рекомендуем использовать нашу систему заданий в начальных классах. Наука шагнула вперёд, а учебно-методические комплексы во многом отстают, не освещают многие темы на должном уровне, но от этого не должны страдать дети, ученики.

Теперь ученики не путают «многогранник» с другими фигурами, такими как «многоугольник».

Заключение.

В современных обучающих программах начальной школы важное значение придаётся логической составляющей. Развитие логического мышления ребёнка подразумевает формирование логических приёмов мыслительной деятельности, а также умения понимать и прослеживать причинно-следственные связи явлений и умений выстраивать простейшие умозаключения на основе причинно - следственной связи.

Развитие логики и мышления является неотъемлемой частью гармоничного развития ребёнка.

Мы рассмотрели первый компонент познавательной дея­тельности - логические приемы мышления. Важность их фор­мирования у учащихся не требует доказательств, это очевид­но. Именно поэтому задача формирования логического мыш­ления ставится перед всеми учителями, при изучении всех предметов. Однако такая общая постановка задачи явно не­достаточна. Как мы видели, логическое мышление нельзя формировать с любого приема: они связаны между собой внутренней логикой, поэтому могут быть сформированы только в оп­ределенной последовательности.

Мы ставили перед собой проблему: можно ли использовать разработанную нами систему упражнений для развития в большей степени абстрактного мышления у учащихся, учить логическим приёмам.

Проведённое нами исследование показало и доказало, что разработанную нами систему упражнений можно и нужно применять на практике.

Проведённые нами исследования показали, что у большей части учащихся 4 классов не сформировано понятие многогранников. Многие ученики знают некоторые логические приёмы, но не умеют использовать их на практике, применять. Ученики за частую не умеют дифференцировать отдельные стороны предметов, в результате чего изменение одного свойства он принимает за изменение другого. Иногда ученики путают многогранники с многоугольниками и наоборот. Учащиеся допускают еще больше ошибок при выполнении классификаций, при выведении следствий из данных посылок. В то же время, как показывают исследования, многие из этих приемов учащиеся могут успешно усвоить уже в начальной школе, если работу вести планомерно и целенаправленно.

Вывод, который вытекает из всего вышесказанного, за­ключается в том, что уже в начальной школе при построении содержания обучения необходимо предусмотреть всю систему логических приемов мышления, необходимых для работы с планируемыми предметными знаниями, для решения задач, предусмотренных целями обучения. При этом важно отметить, что хотя логические приемы формируются и используются на каком-то конкретном предметном материале, в то же время они не зависят от этого материала, носят общий, универсаль­ный характер. В силу этого логические приемы, будучи усвое­ны при изучении одного учебного материала, могут в даль­нейшем широко применяться при усвоении других учебных предметов как готовые познавательные средства.

Следовательно, при отборе логических приемов, которые должны быть усвоены при изучении какого-то предмета, сле­дует учитывать межпредметные связи. Если какие-то логиче­ские приемы мышления были сформированы ранее - при изу­чении предыдущих предметов, то при усвоении данного пред­мета нет необходимости формировать их заново. Эти приемы просто используются для усвоения данных знаний. Предме­том специального усвоения должны быть только такие логи­ческие приемы, с которыми учащиеся встречаются впервые.

Методические рекомендации:

1. Повышать уровень знаний у учителей в области геометрии и логики для начальных классов.

2. Использовать разработанную нами систему заданий.

3. Использовать учебно-методические пособия И.В. Шадриной - геометрия в начальных классах в своей работе.

Список литературы:

1. Бантова М.А, Бельтюкова Г.В. Методика начального обучения математики в начальных классах. - М: Просвещение, 1984.-234с

2. Волкова С.И., Столярова Н.Н. Развитие познавательных способностей детей на уроках математики в 3 кл. (1-4). - Просвещение, 1997. Математика и конструирование. Интегрированный курс -254с

3. Выготский Л.С. Вопросы детской психологии СПб.: Союз,1997.-224с

4. Гетмонова А.Д. Учебник по логике.-М, «Черо»,2000г.-303с.

5. Гетмонова А. Д.Занимательная логика.Ч1-М., «Владос»,1998г.-239 с

6. Гетмонова А. Д.Логика. Словарь и задачник.-М, «Владос», 1998г,-334с

7. Давыдов В. В. , Кудрявцев В. Т. : Развивающее образование: теоретические основания преемственности дошкольной и начальной школьной ступеней 97'1 с.3

8. Дрозд В.А. и др. Методика начального обучения математике. -Минск, 1988-156с

9. Закон РФ «об образовании» от 10.07.1992 N 3266-1

10. Ивин А.А. Искусство правильно мыслить. М.: Просвещение, 1990.-220с

11. Лев Семенович Выгодский – Лекции по психологии- 1. Восприятие; 2. Память; 3. Мышление; 4. Эмоции; 5. Воображение; 6. Проблема воли-1932г-510с

12. Левитов Н.Д. Детская и педагогическая психология. М., 1960.-214с

13. Липкина Л.И.Психология ребёнка и формирование нравственных компонентов его мировоззрения- НИИ общей и педагогической психологии АПН СССР, Москва

14. Математика: 1 класс: Поурочные разработки к учебнику М.И.Моро, С.И.Волкова, С.В.Степанова "Математика: 1 класс: В 2 ч." автор книги. Бахтина С.В.-210с

15. Математика 4 класс. Методика обучения Рудницкая В.Н.- Вентана-Граф.-М.:2005г-192с

16. Математика. 4 класс. Рабочая тетрадь (под редакцией М. В. Богдановича) 123-Н6345Р-122с

17. Маркова А.К. Формирование мотивации учения в школьном возрасте. М.: Просвещение, 1996.-114с

18. Моро М.И. и др. Математика: 1-4 класс.- М.: Просвещение, 1993

19. Немов С.С. Психология: Учебник для студентов высш.пед.учеб.заведений. В 3х кн., кн. 2. Психология образования.- 3е издание.-М.: Гуманист. Изд. центр Владос, 1998.-608с.

20. Общая психология: учеб. для студентов пед. ин-тов / под ред. А. В. Петровского. – М.: Просвещение, 1986.

21. Педагогика. Учеб.пособие для студентов пед.вузов п пед колледжей./ Под ред. П.И. Пидкасистого. - М.: Просвещение,1982. - 160с.

22. Развитие младших школьников в процессе усвоения знаний/Под ред. Н.В. Зверевой. М.: Педагогика, 1995.-160с

23. Стойлова Л.П., Пышкало А.М. Основы начального курса математики. М.: Просвещение, 1988.-200с

24. Тиморин В.А. Комбинаторика выпуклых многогранников. — МЦНМО, 2002. — 16 с.

25. Тихомиров, О.К. Психология мышления / О.К. Тихомиров. – М.: Академия, 2002-130с

26. Царёва С.Е. Математика и конструирование. Программа для начальной школы и методические рекомендации учителю.- Новосибирск, 1991.-200с

27. Черемошкина Л. В. Психология мнемических способностей. МПГУ, 2000 г. 19.00.07

28. Шадрина И.Р. Геометрия в начальной школе: учебное пособие для студентов факультетов начальных классов.-М.;МГПУ,2007г-175с

29. Шарыгин, И.Ф. Задачи по геометрии (Планиметрия) / И.Ф. Шарыгин. – М.: Наука, 1986-210с

малый додекаэдр

большой звездчатый додекаэдр

большой икосаэдр

Тема: Многоугольники и многогранники.

Цель: Обобщить у учеников имеющиеся знания. Формировать общие представления о «многогранниках».

Этапы урока	Деятельность учителя	Деятельность учеников
Орг. момент	Приветствие. Настрой на работу	Приветствие. Настрой на работу
Подготовка к изучению нового материала.	На доске: И несколько др. многоугольников и многогранников. Посмотрите внимательно на эти фигуры. На какие две группы мы их можем разделить?	Ученики рассматривают предложенные фигуры Плоские и объёмные фигуры
Изучение нового материала.	Совершенно верно. А вы знаете, как называются представленные здесь плоские фигуры? Что же такое многоугольник? Многоугольник- это геометрическая фигура, имеющая 3 и более углов. Само название фигур вам подсказывает, что это за фигура. А может ли быть у многоугольника два угла? Решив проблемную задачу, приходим к выводу, что не бывает многоугольников с двумя углами. Какие многоугольники вы знаете? Напоминаю, что треугольник – это тоже многоугольник.	Возможно, кто-то расскажет, что это многоугольники. Ответы детей. Те, кто ответил да выходят к доске и пытаются такую фигуру построить. Перечисляют, знакомые им многоугольники.
Практическое задание.	Постройте на розданных вам листочках, многоугольник, который вам больше нравится.	Строят каждый свой многоугольник.
Продолжение работы над темой урока.	А как называются объёмные тела представленные на доске? Что же такое многогранник? Если получен ответ, что это фигура, имеющая много граней, то подвожу к тому, чем же являются эти грани, а они являются многоугольниками. Многогранник – это тело, граница которого состоит из многоугольников. Эти многоугольники называются гранями, их стороны — рёбрами, а их вершины — вершинами многогранника. Рассматриваем несколько моделей многогранников. Разбираем, где находятся грани, вершины, рёбра.	Возможно, кто-то из учеников ответит, что фигуры называются многогранники. Ученики пытаются сами ответить. Один из ответов –это фигура имеющая много граней. Рассматривают несколько моделей многогранников. Разбирают, где находятся грани, вершины, рёбра.
Практическое задание.	Каждая пара учеников получила модель многогранника. Задание: Разными цветами (карандашами, фломастерами) указать на модели где у этого многогранника грани, вершины, рёбра.	Выполняют по парам, после окончания выполнения задания выходят и рассказывают, показывают остальным ученикам.
Из истории многогранников. Подведение итогов.	Учитель рассказывает про многогранники: Существует несколько видов многогранников: тетраэдр, гексаэдр (куб), октаэдр, додекаэдр, икосаэдр. Почему правильные многогранники получили такие имена? Это связано с числом их граней. Тетраэдр имеет 4 грани, в переводе с греческого "тетра" - четыре, "эдрон" - грань. гексаэдр (куб) имеет 6 граней, "гекса" - шесть; октаэдр - восьмигранник, "окто" - восемь; додекаэдр - двенадцатигранник, "додека" - двенадцать; икосаэдр имеет 20 граней, "икоси" - двадцать. Показывает сложные многогранники: малый и большой додекаэдр. О чём мы сегодня говорили? Что нового вы узнали? Вам понравился урок?	Слушают рассказ учителя. Рассматривают предложенные многогранники. Отвечают на вопросы.

Тема: Прямоугольный параллелепипед и Куб.

Цель: Формирование представлений о прямоугольном параллелепипеде.

Этапы урока	Содержание деятельности учителя	Содержание деятельности учеников
1.Орг. момент. 2. Устный счёт. 3. Подготовка к изучению нового материала. 4. Постановка целей и задач урока. 5. Работа над новой темой урока. 6. Работа в рабочих тетрадях. 7. Работа над новой темой урока (продолжение). 8. Работа с учебником. 9.Решение задачи 10.Подведение итогов	Здравствуйте, меня зовут Светлана Александровна. Садитесь. У нас сейчас урок математики. Проверьте вашу готовность к уроку. На парте у вас: учебник, тетрадь, рабочая тетрадь, пенал. У каждого из вас на доске лежит таблица, используя алгоритм который вы видите на доске, решите примеры. Полученный результат запишите в таблицу. 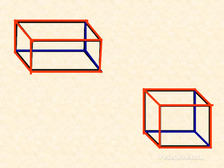На доске: Слайд №2. Показываю изображения тел и фигур. На какие две группы мы можем разделить эти фигуры? Чем отличаются? 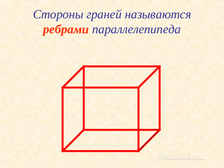Вы уже начали знакомиться с объёмными фигурами, которые называются многогранники. Что такое многогранник? Сегодня мы продолжим знакомство с многогранниками. Слайд № 3 Кто знает, какая из этих фигур называется прямоугольным параллелепипедом? Многогранник, который имеет такую же форму, как например, коробка сахара, кирпича, ящика, называют прямоугольным параллелепипедом. Слайд № 4. Какие ещё предметы имеют форму прямоугольного параллелепипеда? Видите, вы каждый день сталкиваетесь с прямоугольным параллелепипедом. Давайте вспомним, что такое грань многогранника? Где же находятся грани у прямоугольного параллелепипеда? Какая фигура, является гранью прямоугольного параллелепипеда? Сколько граней у прямоугольного параллелепипеда? Слайд № 5. Есть ли у него равные грани? Какие? Кто знает, почему прямоугольный параллелепипед так называется? Сейчас мы вместе сосчитаем и назовём грани прямоугольного параллелепипеда. Слайд № 6-8. Что такое ребро многогранника? 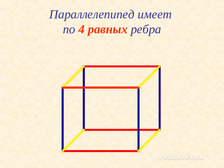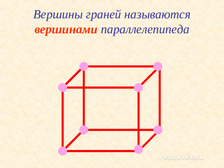Стороны граней называются ребрами параллелепипеда. Слайд №9. Параллелепипед имеет по 4 равные ребра. Слайд №10. Что такое вершины многогранника? Слайд №11. Вершины граней называются вершинами параллелепипеда. Давайте ещё раз повторим, где у прямоугольного параллелепипеда грани, рёбра и вершины. Для этого откройте ваши рабочие тетради стр. 33. Выполните самостоятельно № 107. Ещё раз проговариваем, что такое грани, рёбра и вершины. Как на чертеже обозначаются видимые рёбра? Не видимые? Выполните самостоятельно № 108. Почему этот прямоугольный параллелепипед называется кубом? Докажите. Откройте учебники на стр. 48. № 169. Назовите рёбра, которые выходят из вершины А? Назовите рёбра, которые выходят из вершины K? Как эти вершины можно назвать, одним словом? Назовите каждое видимое ребро? Назовите пары равных граней? №170 Как находится площадь прямоугольника? Теперь решим задачу. Стр.46 №163 Прочтите условие. Давайте вспомним формулы, которые нам могут понадобиться. Давайте составим таблицу: t V S проплыли 2ч 4км/ч ? пешком 3ч 6км/ч ? Для заполнения таблицы: Что нам известно? Какое ещё время известно? Какая скорость у туристов была, когда они плыли на плоту? Какая скорость была, когда туристы шли пешком? Что нам нужно узнать? Какой вопрос в задаче? Что будем узнавать в первом действии? Что для этого нужно сделать? Что будем узнавать во втором действии? Что для этого нужно сделать? Как же найти длину всего маршрута? Ответ: 26 км длина всего пути. Какие фигуры мы сегодня изучали? Почему эти фигуры так называются? Сколько граней? Рёбер? вершин? Если останется время, то № 109 стр.33 в рабочих тетрадях, № 171 стр. 48 в учебниках	Здороваются, садятся. Проверяют свою готовность к уроку. У каждого перед собой: 590 890 707 55 90 199 290 99 Слайд №2. Объёмные и не объёмные. Фигура, поверхность, которой состоит из многоугольников, называются многогранниками. Дети высказывают своё мнение. Называют предметы указанной формы из быта, своей жизни. Каждый из многоугольников называют гранью многогранника. Гранью прямоугольного параллелепипеда является прямоугольник. 6 Показывает на модели. Все грани – прямоугольники. Стороны многоугольников называют гранями многогранника. Показывает на модели. Вершины многоугольника- вершины многогранника. Проверка: Слайд № 12. Выполняют самостоятельно. Потому, что грани – квадраты. Квадрат – это прямоугольник, у которого все стороны равны. AB,AE,AD KE,KP,KD Невидимые AB,BM,AE,EM,AD,DC,BC,CP,MP Называют S=a*b S = V · t V = S : t t = S : V Отвечают на вопросы – заполняем таблицу Узнаем расстояние, которое туристы проплыли Скорость умножить на время Узнаем расстояние, которое туристы прошли пешком Скорость умножить на время Найти сумму двух отрезков пути. Прямоугольный параллелепипед, куб 6, 12, 8

Тема: Развёртка многогранников.

Цель: Формировать представление о развёртке многогранников (практическое занятие).

Этапы урока	Деятельность учителя	Деятельность учеников.
1.Орг. момент. 2.Повторение изученного материала. 3.Постановка целей и задачей урока. 4.Выполнение заданий. 5.Практическое задание. 6.Итог урока. 7. Домашнее задание.	Приветствие. Настрой на работу. Вопросы по пройденному материалу. Про многогранники и их части, прямоугольный параллелепипед, куб. М ы с вами уже много говорили про многогранники. Каждый многогранник, можно «развернуть», в результате чего получится плоская фигура, состоящая из нескольких многоугольников. Показываю развёртку куба. У каждого многогранника есть развёртка. Сейчас мы выполним несколько заданий, что бы вы знали каким многогранникам, какие развёртки соответствуют. Задания в презентации. В презентации были представлены такие задания: Какая из предложенных фигур соответствует данной развёртке; Какая развёртка соответствует данной фигуре; Какая фигура получится из данной развёртки. Использовались разные многогранники. Заштриховывались разные грани этих многогранников, для усложнения заданий. Показываю видеофильм про развёртку куба. У каждого из вас на столе лежит развёртка куба. Давайте сами соберём свой многогранник – куб. Для работы нам понадобятся: клей, развёртка куба и ваша внимательность. У кого нет клея даю или прошу поделиться клеем соседа. Наглядно на развёртке больше чем у ребят показываю, как склеить куб. Что сегодня на уроке мы с вами делали? Что вы узнали нового? Составить развёртку к шестиугольной пирамиде. По желанию.	Приветствие. Настрой на работу. Отвечают на вопросы учителя. Слушают рассказ учителя. Рассматривают развёртку куба. Выполняют вместе с учителем задания. У каждого на парте клей и развёртка куба. Все готовы к работе. Смотрят на образец учителя, самостоятельно склеивают модель куба из развёртки.

Тема: Многогранники и многоугольники.

Цель: Закрепление пройденного материала.

Этапы урока	Деятельность учителя	Деятельность учеников.
1.Орг. момент. 2.Проверка домашнего задания. 3. Повторение изученного материала. 4.подведение итога.	Приветствие. Настрой на работу. Ученикам было заданно составить развёртку шестиугольной пирамиды. Проверили правильность выполнения задания при помощи презентации. Мы с вами очень много говорили про многогранники. Я думаю, вы много узнали нового и многое запомнили. Давайте проверим. Выполняем задания из презентации. В презентации задания такого типа: Из знакомых нам многогранников был составлен рисунок. Какие многогранники вы тут видите? Проверку выполнения заданий проведена в самой презентации. Теперь ответьте мне на несколько вопросов. Что такое многоугольник? Что такое многогранник? А как мы называем эти многоугольники? Совершенно верно. Какие вы знаете многогранники? После выявления знакомых многогранников, обсуждали их, находили грани, рёбра, вершины. Говорили, о том какая фигура лежит в основании. А где мы встречаем многогранники в обычной жизни? Вам понравилось занятие? Чем занимались на сегодняшнем занятии?	Приветствие. Настрой на работу. Ученики с учителем проверили правильность выполнения задания. Выполняют задания, отвечают на вопросы учителя. Многоугольник- это геометрическая фигура, имеющая 3 и более углов. Само название фигур вам подсказывает, что это за фигура. Многогранник – это тело, граница которого состоит из многоугольников. Эти многоугольники называются гранями, их стороны — рёбрами, а их вершины — вершинами многогранника. Называют несколько многогранников. Вместе с учителем ещё раз разбирали части многогранников. Приводят примеры, где видели многогранники и что это были за многогранники. Отвечают на вопросы учителя.