Презентация и технологическая карта к уроку информатики по теме "Решение задач с помощью графов"; 7 класс

Технологическая карта урока

«Решение задач с помощью графов»

Предмет		Информатика
Класс		7
Тема урока		Решение задач с помощью графов
№ урока по теме		5
Тип урока		Применение полученных знаний, элементы проблемного
Цель урока		Научить использовать терминологию связанную с графами, решать задачи по графам
Планируемые результаты (личностные, предметные, метапредметные)		Познакомиться с примерами использования графов, деревьев и списков при описании реальных объектов, научить ставить цель на основе определенной проблемы и существующих возможностей, объяснять связи и отношения, играть определенную роль в совместной деятельности
Основные понятия темы		Графы, ребро, дуга, дерево
Интернет-ресурсы к уроку
Технология изучения
Этап занятия	Деятельность учителя		Деятельность обучающихся
I. Организационный момент	Приветствие учащихся, проверка готовности к уроку		Приветствие учителя
II. Этап проверки выполнения домашнего задания 4 мин	Компьютер учителя, проектор, экран
	Открывает презентацию и задает задание, найти в кроссворде все понятия, связанные с графами, на выбор соседа дать определение 2-3 понятиям		Индивидуальная работа учащихся по поиску основных понятий.
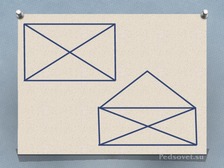
Этап усвоения новых знаний и способов действий 12 мин	Постановка проблемной ситуации. Предлагает две фигуры и ставит вопрос: можно ли нарисовать эти фигуры одним росчерком пера? показать как это сделать		Один учащийся выполняет задание на доске. Отвечают на вопрос, рисуют фигуры
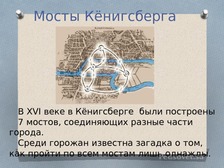
	Задает вопрос можно ли каким то способом, без рисования, узнать нарисуются фигуры одним росчерком пера или нет. Чтобы ответить на этот вопрос, обратимся к истории и вспомним задачу про Кенигсбергские мосты. Формулирует задачу, коротко рассказывает о Л.Эйлере и его теории графов.		Мозговой штурм. Предлагают ответы. Предполагают решение задачи о мостах. Обосновывают выбор.
			Делают выводы по мостам и рисованию фигур.
	Объявляет тему урока. Наша задача сегодня научиться решать задачи с помощью графов.
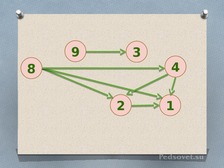
	Объясняет технологию решения задач. Разбирает 1 задание с учащимися		Работа по образцу. Строят граф
Этап первичной проверки понимания изученного 5 мин	Проверяет решение задания 2		Самопроверка. Самостоятельно выполняют 2 задание, задают вопросы.
Этап закрепления новых знаний и способов действий 4 мин	Проверяет решение задания 3		Взаимопроверка. Самостоятельно выполняют 3 задание, задают вопросы.
Этап применения знаний и способов действий 6 мин	Проверяет решение задания 4		Практическая работа на компьютере. Решение 4 задания оформляют в виде схемы в MS Word.
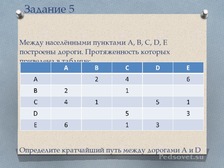
Этап контроля и самоконтроля знаний и способов действий 5 мин	Пока учащиеся медленно выполняющие 4 задание его доделывают, с успешно его выполнившими разбирает задание 5		Один учащийся у доски выполняет задание, остальные проверяют

Этап информации о домашнем задании 2 мин	Придумать или найти в интернете загадки, о фигурах соединяемых одним росчерком пера. Задачи 4,6 после параграфа 5		Записывают д/з
Этап подведения итогов занятия 1 мин	1 смайл – урок понравился, узнал что-то новое 2 смайл – узнал немного, урок понравился 3 смайл – ничего нового не узнал или урок не понравился		На маркерной доске оставляют номер смайла: 1,2 или3

Слайд 1

Графы

Слайд 2

р л с а а н н ы е б п г в д е й о р д у о е р в р о д и р в о е и е н т и и ш р г р а ф а н к н

Слайд 3

Слайд 4

Слайд 5

История появления теории Годом зарождения теории графов считается 1736-й, когда математик Леонард Эйлер опубликовал в Санкт-Петербургской Академии наук работу, посвящённую семи мостам города Кёнигсберга.

Слайд 6

Мосты Кёнигсберга В XVI веке в Кёнигсберге были построены 7 мостов, соединяющих разные части города. Среди горожан известна загадка о том, как пройти по всем мостам лишь однажды.

Слайд 7

Мосты Кёнигсберга Для решения этой задачи Эйлер вводит понятие «графа» как множества непересекающихся рёбер или связей, соединяющих пары

Слайд 8

Характеристики графа O Если все вершины графа четные, то можно одним росчерком пера начертить граф. При этом начать движение можно с любой вершины и закончить в той же вершине O Граф с двумя нечетными вершинами также можно начертить одним росчерком. Начинать движение надо с одной нечетной вершины, а заканчивать в другой. O Граф с большим количеством нечетных вершин невозможно начертить таким образом

Слайд 9

Задание 1 Начертите граф , на котором были бы изображены высказывания: «8 кратно 2» «9 кратно 3» «8 кратно 1» «4 кратно 2» «8 кратно 4» «4 кратно 1» «2 кратно 1» Каждая стрелка графа должна обозначать «кратно».

Слайд 10

9 3 4 8 2 1

Слайд 11

«Социальные сети» Задание 2 В социальной сети Дима дружит с Юрой, Толей, Аленой, Леной и Машей. Лена дружит с Машей, а Алена с Юрой. Профили всех ребят закрытые, т.е. просматривать сообщения друг у друга могут только друзья. У кого из друзей на стене может оставить секретное послание Дима, не опасаясь, что об этом узнают остальные? Могут ли девочки общаться, сохраняя свои секреты от ребят?

Слайд 12

Задание 3 Между планетами Солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: OЗемля – Меркурий; OПлутон – Венера; OЗемля – Плутон; OПлутон – Меркурий; OМеркурий – Венера; OУран – Нептун; OНептун – Сатурн; OСатурн – Юпитер; OЮпитер – Марс O Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса ?

Слайд 13

Задание 4 Всего существует 4 группы крови. При переливании крови от одного человека к другому не все группы совместимы. Известно, что кровь первой группы совместима со всеми остальными. Но человек с 1 группой воспринимает только кровь своей группы. Носителю 4 группы можно переливать любую другую, но кровь 4 группы можно переливать только в 4 группу и больше никому. Также все группы совместимы сами с собой. Начертите граф, который бы изображал возможные варианты переливания крови.

Слайд 14

Слайд 15

Задание 5 Между населёнными пунктами A, B, C, D, E построены дороги. Протяженность которых приведена в таблице: Определите кратчайший путь между дорогами A и D.

Слайд 16

1 2 3

Полный текст материала Презентация и технологическая карта к уроку информатики по теме "Решение задач с помощью графов"; 7 класс смотрите в скачиваемом файле.
На странице приведен фрагмент.

Автор: Хаметова Людмила Алексеевна → hla9969

18.11.2016

5124

458

Комментировать

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.

Вход | Регистрация

запомнить
Забыл пароль \| Регистрация