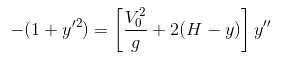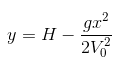|
Тема для вопросов по физике, астрономии и математике.
|
|
|
ФИАН-5 | Дата: Пятница, 02.02.2018, 12:04 | Сообщение # 46 |
ФИАН-5
Ранг: Дошколенок (?)
Группа: Заблокированные
Должность: Учитель физики
|
| Сообщений: |
2 |
| Награды: |
0 |
| Статус: |
Offline |
|
Цитата ФИАН (  ) Вообще можно записать интересное уравнение для определения высоты отрыва, если форма поверхности задана уравнением y=y(x). Это немного не школьный момент, но если будет интерес, напишу и объясню.
Основные моменты и обозначения.
Форма горки представляет собой поверхность вращения графика y(x) при x>=0 вокруг оси OY. Максимальная высота горки H, шайба на максимальной высоте имеет скорость Vo, направленную по касательной к поверхности. Введём безразмерные переменные:
U=Hx
V=Hy
s=Vo^2/2gH
V=V(U).
Условие отрыва шайбы от поверхности, то есть обращение в ноль нормальной реакции поверхности в некоторой точке, может быть записано в виде.
- (1 + (V’)^2) = 2 (s + 1 – V)V’’.
Здесь V’ и V’’ суть первая и вторая производные V(U) по U. Первая производная определяет угол наклона касательной к поверхности в данной точке, вторая производная «пришла» из выражения для кривизны линии V(U), известной из дифференциальной геометрии.
Это уравнение позволяет определить ту точку или высоту на поверхности, в которой и происходит отрыв. Например, в том случае, когда форма поверхности эллиптическая
(U/a)^2 + V^2 = 1,
высота отрыва
Vотрыва = 2(s +1)/(2 + a^2).
Для окружности а=1 и при s=1 (соскальзывание без начальной скорости) V=2/3 – известный результат.
Есть линия, при движении по которой в любой её точке выполняется условие отрыва, то есть шайба нигде на «давит» на поверхность. Можно догадаться, что такой линией является парабола, по которой движется брошенная горизонтально шайба:
V = 1 – U^2/4s.
На этом можно остановиться.
02.02.2018
|
|
|
|
| |
|
|
drakonchikded | Дата: Четверг, 22.03.2018, 11:22 | Сообщение # 47 |
| Сообщений: |
45 |
| Награды: |
1 |
| Статус: |
Offline |
|
Цитата ФИАН-5 (  ) Условие отрыва шайбы от поверхности, то есть обращение в ноль нормальной реакции поверхности в некоторой точке, может быть записано в виде.
- (1 + (V’)^2) = 2 (s + 1 – V)V’’.
Позволю себе вставить свои 5 копеек.
Сделал выкладки.
Да, именно такое уравнение получается (только я использовал не безразмерные величины,
а обычные, более привычные):
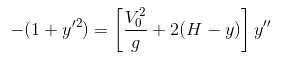
Можно найти производные выбранной кривой, подставить в это уравнение и решить его потом как алгебраическое.
Что и показал ФИАН-5 в своем сообщении. При этом будет найдена единственная точка отрыва.
А можно исходно смотреть на него как на дифур, который нужно решить.
Решение дает ровно ту кривую,
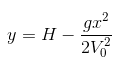
о которой писал ФИАН-5:
Цитата ФИАН-5 (  ) Можно догадаться, что такой линией является парабола, по которой движется брошенная горизонтально шайба:
V = 1 – U^2/4s.
У неё каждая точка является точкой отрыва.  Добавлено (22.03.2018, 11:22)
---------------------------------------------
из известной брошюры В.И.Арнольда:
Гипотенуза прямоугольного треугольника (в американском стандартном экзамене) — 10 дюймов, а опущенная на нее высота — 6 дюймов. Найти площадь треугольника. С этой задачей американские школьники успешно справлялись 10 лет, но потом приехали из Москвы русские школьники, и ни один эту задачу решить не смог.

22.03.2018
Сообщение отредактировал drakonchikded - Суббота, 03.02.2018, 01:18
|
|
|
|
| |
|
|
iyugov | Дата: Четверг, 22.03.2018, 15:50 | Сообщение # 48 |
iyugov
Ранг: Доцент (?)
Группа: Активисты
Должность: Инженер, учитель
|
| Сообщений: |
1191 |
| Награды: |
12 |
| Статус: |
Offline |
|
Цитата drakonchikded (  ) Гипотенуза прямоугольного треугольника (в американском стандартном экзамене) — 10 дюймов, а опущенная на нее высота — 6 дюймов. Найти площадь треугольника. С этой задачей американские школьники успешно справлялись 10 лет, но потом приехали из Москвы русские школьники, и ни один эту задачу решить не смог.
Как-то на контрольной по алгебре мне, ученику, попалась задача примерно следующего содержания: "Одна из сторон прямоугольного треугольника вдвое больше другой стороны и втрое больше третьей, а периметр треугольника равен 55 см. Найти меньшую сторону треугольника". Я тоже не смог её решить.
22.03.2018
Сообщение отредактировал iyugov - Четверг, 22.03.2018, 15:51
|
|
|
|
| |
|
|
drakonchikded | Дата: Пятница, 23.03.2018, 09:04 | Сообщение # 49 |
| Сообщений: |
45 |
| Награды: |
1 |
| Статус: |
Offline |
|
Цитата iyugov (  ) Школьники из Москвы не изучали комплексные числа?
Скорее наоборот...Добавлено (23.03.2018, 09:04)
---------------------------------------------
Добавлю. Я ситуацию понял так: американские школьники тупо механически применили
формулу площади, а русские стали вдумываться, и поняли, что таких треугольников
не существует.
Аналитически проанализировать ситуацию просто. Пусть Х и У - катеты.
Очевидно, что
Х2+У2=100
2ХУ=120
Вычтя второе из первого, получим
(Х-У)2 = -20
Геометрически ещё проще.
Рассмотрим множество прямоугольных треугольников, вписанных в окружность с диаметром,
равным гипотенузе. Очевидно, что максимально возможная величина высоты,
опущенной на гипотенузу, равна половине гипотенузы.
23.03.2018
|
|
|
|
| |
|
|
iyugov | Дата: Пятница, 23.03.2018, 19:46 | Сообщение # 50 |
iyugov
Ранг: Доцент (?)
Группа: Активисты
Должность: Инженер, учитель
|
| Сообщений: |
1191 |
| Награды: |
12 |
| Статус: |
Offline |
|
drakonchikded, это вообще похоже на байку в стиле "ну, тупые" сатирика Задорнова.
Ну, а что... если переменный ток обсчитывают комплексными числами, то почему треугольнику с комплексными сторонами нельзя придать смысл?
23.03.2018
|
|
|
|
| |
|
|
drakonchikded | Дата: Пятница, 23.03.2018, 21:35 | Сообщение # 51 |
| Сообщений: |
45 |
| Награды: |
1 |
| Статус: |
Offline |
|
Цитата iyugov (  ) почему треугольнику с комплексными сторонами нельзя придать смысл?
Можно. А смысл? 
23.03.2018
|
|
|
|
| |
|
|
iyugov | Дата: Суббота, 24.03.2018, 11:32 | Сообщение # 52 |
iyugov
Ранг: Доцент (?)
Группа: Активисты
Должность: Инженер, учитель
|
| Сообщений: |
1191 |
| Награды: |
12 |
| Статус: |
Offline |
|
drakonchikded, некоторые задачи с треугольниками решаются через векторы и через комплексные числа. Правда, стороны там обычно комплексные, а их длины всё ещё действительные.
24.03.2018
|
|
|
|
| |
|
|
drakonchikded | Дата: Воскресенье, 25.03.2018, 00:06 | Сообщение # 53 |
| Сообщений: |
45 |
| Награды: |
1 |
| Статус: |
Offline |
|
iyugov, применение комплексных чисел для решения треугольников никто не отрицает
как альтернативный метод. Но речь ведь зашла о треугольнике (см сообщение 47), у которого
именно длины катетов выражаются комплексными числами. Такой треугольник не построишь
с помощью циркуля и линейки, потому что он не существует. И с помощью комплексных чисел
его не вытащить из небытия. Непонятно, для чего Вы о них вспомнили...
25.03.2018
|
|
|
|
| |
|
|
iyugov | Дата: Воскресенье, 25.03.2018, 09:52 | Сообщение # 54 |
iyugov
Ранг: Доцент (?)
Группа: Активисты
Должность: Инженер, учитель
|
| Сообщений: |
1191 |
| Награды: |
12 |
| Статус: |
Offline |
|
drakonchikded, я бы не стал утверждать, что вот прямо никак не вытащить. Неевклидову геометрию тоже трудновато реализовать циркулем и линейкой. Может, мы просто не знаем возможного применения. В вузе я понял, что и в ТОЭ, и в ТАУ комплексные числа применяются достаточно широко, чтобы такое предполагать.
Но ладно, это общие рассуждения, а я больше сомневаюсь в том, что описанное Арнольдом событие имело место. В моём классе, например, проблемы с геометрическим смыслом ответа были только у меня. Правда, я не в Москве учился.
25.03.2018
|
|
|
|
| |
|
|
drakonchikded | Дата: Воскресенье, 25.03.2018, 10:26 | Сообщение # 55 |
| Сообщений: |
45 |
| Награды: |
1 |
| Статус: |
Offline |
|
Цитата iyugov (  ) я бы не стал утверждать, что вот прямо никак не вытащить.
Можно, конечно, при достаточной "бурбакизации". 
Можно рассмотреть, например, в абстрактной области, треугольник "шляпка, салат и трагедия" ©
и придать ему некоторый вполне определенный смысл. Серьёзно, без иронии. 
Просто изначально речь шла о сермяжном треугольнике, который можно начертить
или "выстрогать из доски". 
Цитата iyugov (  ) В вузе я понял, что и в ТОЭ, и в ТАУ комплексные числа применяются достаточно широко, чтобы такое предполагать.
Наличие пресловутой "мнимой единицы" определяет правила преобразования реальных величин,
но не делает эти величины (ток, напряжение, мощность, etc) мнимыми (на этом многие спекулируют),
т.к. они, являются всего лишь действительными коэффициентами при i
Вообще, выражение "мнимая единица" крайне неудачно. Порождает много спекуляций.
25.03.2018
|
|
|
|
| |
|
|
iyugov | Дата: Воскресенье, 25.03.2018, 11:48 | Сообщение # 56 |
iyugov
Ранг: Доцент (?)
Группа: Активисты
Должность: Инженер, учитель
|
| Сообщений: |
1191 |
| Награды: |
12 |
| Статус: |
Offline |
|
drakonchikded, да, всё так.
Вот какой ещё вопрос. Есть уравнение:
sqrt(-x^2-1)*0=0.
Какие у него решения в действительных числах согласно школьным правилам?
У меня два варианта:
- все действительные числа, т. к. после извлечения корня даже комплексные числа, умноженные на ноль, дают ноль;
- решений нет, т. к. промежуточное выражение с извлечением корня при любых действительных значениях x считается "не имеющем смысла".
25.03.2018
|
|
|
|
| |
|
|
Миклухо | Дата: Воскресенье, 25.03.2018, 20:01 | Сообщение # 57 |
Миклухо
Ранг: Профессор (?)
Группа: Я - учитель
|
| Сообщений: |
3504 |
| Награды: |
101 |
| Статус: |
Offline |
|
Цитата iyugov (  ) а я больше сомневаюсь в том, что описанное Арнольдом событие имело место.
Не сомневайтесь. Только-что проделал эксперимент:
https://cont.ws/@mikluho/891816
Полсуток никто не видел ошибки (с подсказкой), при полутора тысячах просмотров.
25.03.2018
|
|
|
|
| |
|
|
iyugov | Дата: Воскресенье, 25.03.2018, 22:10 | Сообщение # 58 |
iyugov
Ранг: Доцент (?)
Группа: Активисты
Должность: Инженер, учитель
|
| Сообщений: |
1191 |
| Награды: |
12 |
| Статус: |
Offline |
|
Миклухо, эксперимент показал, что эту задачу могут решить далеко не все русскоговорящие. Что, впрочем, и так ясно. Я видел десятки задач, которые почти никто не мог решить; некоторые задачи снабжались пояснениями, что, мол, эту задачу задают на собеседовании в Google, или что её сочинил лично Эйнштейн, или что её не могут решить 99% людей... В совокупности с подразумеваемым противопоставлением России и США вся история оказывается похожей на фейк. Да, и до распространения интернета, в 90-х, в печатных изданиях я видел немало вещей, впоследствии оказавшихся дезинформацией. На что ссылается Арнольд?
25.03.2018
|
|
|
|
| |
|
|
drakonchikded | Дата: Понедельник, 26.03.2018, 14:04 | Сообщение # 59 |
| Сообщений: |
45 |
| Награды: |
1 |
| Статус: |
Offline |
|
Цитата iyugov (  ) Какие у него решения в действительных числах согласно школьным правилам?
Школа школе рознь.
Цитата iyugov (  ) У меня два варианта:
В зависимости от школы можно либо тот, либо другой, а можно и тот, и другой.
И всё это равноправные школы, парящие над полями чисел, - каждая над своим.

26.03.2018
|
|
|
|
| |
|
|
iyugov | Дата: Понедельник, 26.03.2018, 17:20 | Сообщение # 60 |
iyugov
Ранг: Доцент (?)
Группа: Активисты
Должность: Инженер, учитель
|
| Сообщений: |
1191 |
| Награды: |
12 |
| Статус: |
Offline |
|
drakonchikded, понятно, что подходы к решению могут быть разные. Но судя по этой теме, они тут неравноправны, потому что некоторые из них плохо стыкуются со знаниями школьников: тут китайская теорема не православная, там безразмерную единицу не используй... Как бы вы решили это уравнение "в действительных числах", предполагая, что надо будет зафиксировать однозначный ответ, а решение надо будет объяснить школьнику?
26.03.2018
|
|
|
|
| |
|