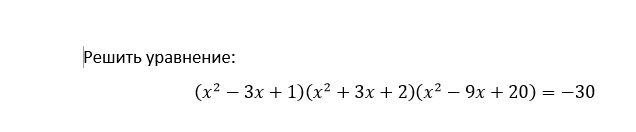|
Любые вопросы по всем формам ГИА - ОГЭ и ЕГЭ
|
|
|
Ralph124s41 | Дата: Среда, 04.05.2016, 10:54 | Сообщение # 466 |
| Сообщений: |
41 |
| Награды: |
0 |
| Статус: |
Offline |
|
Цитата miflin (  ) Как объяснить, например, природу закона Кулона?
Виртуально испускаемые электроны аннигилируют с позитронами, создаётся разрежение, давлением эфира, среды, тонкого мира тела ( с разными зарядами) притягиваются. И не говорите мне про отсутствие эфира - опыты, доказывающие его отсутствие, были некорректны.
04.05.2016
|
|
|
|
| |
|
|
miflin | Дата: Среда, 04.05.2016, 11:48 | Сообщение # 467 |
miflin
Ранг: Профессор (?)
Хмырь обыкновенный
Группа: Пользователи
|
| Сообщений: |
2663 |
| Награды: |
87 |
| Статус: |
Offline |
|
Цитата Ralph124s41 (  ) И не говорите мне про отсутствие эфира
Я с превеликим удовольствием готов "неговорить" с Вами не только об отсутствии эфира,
но и о чем бы то ни было.
04.05.2016
Сообщение отредактировал miflin - Среда, 04.05.2016, 11:59
|
|
|
|
| |
|
|
Ralph124s41 | Дата: Среда, 04.05.2016, 13:36 | Сообщение # 468 |
| Сообщений: |
41 |
| Награды: |
0 |
| Статус: |
Offline |
|
Цитата miflin (  ) Пешеход движется по прямой в южном направлении в течение 1/3 от всего времени движения со скоростью V1=3км/ч.
Затем проходит по прямой треть всего пути в восточном направлении со скоростью V2.
Затем возвращается по прямой в исходную точку.
Найти среднюю скорость пешехода на всём маршруте.
А мне не понравилась. Вот, если бы V2=4 km/h, то был бы египетский тр-к. А вдруг он пойдёт быстро, допустим, 6 км/ч, а оставшуюся часть - спортивной ходьбой?Добавлено (04.05.2016, 13:36)
---------------------------------------------
Цитата miflin (  ) но и о чем бы то ни было.
Извините за то, что ко двору не пришёлся. Обещаю на этом форуме не появляться.
04.05.2016
|
|
|
|
| |
|
|
gail-ul | Дата: Воскресенье, 06.11.2016, 12:38 | Сообщение # 469 |
gail-ul
Ранг: Первоклашка (?)
Группа: Пользователи
|
| Сообщений: |
24 |
| Награды: |
0 |
| Статус: |
Offline |
|
пожалуйста, посоветуйте пособия для того чтобы научиться решать профильные задания в профильном ЕГЭ для самоподготовки. заранее большое спасибо!
Добавлено (06.11.2016, 12:38)
---------------------------------------------
Большое спасибо, что прислали контакты пользователя Александр_Игрицкий для решения моих вопросов!!!
Сколько на форум не зайду с вопросом, всегда помогают. Спасибо вам!
06.11.2016
Сообщение отредактировал gail-ul - Воскресенье, 06.11.2016, 13:24
|
|
|
|
| |
|
|
miflin | Дата: Суббота, 26.11.2016, 20:47 | Сообщение # 470 |
miflin
Ранг: Профессор (?)
Хмырь обыкновенный
Группа: Пользователи
|
| Сообщений: |
2663 |
| Награды: |
87 |
| Статус: |
Offline |
|
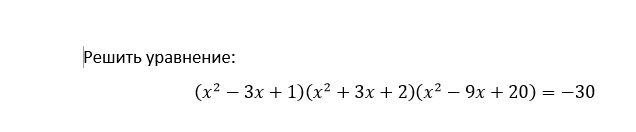
26.11.2016
Сообщение отредактировал miflin - Суббота, 26.11.2016, 20:48
|
|
|
|
| |
|
|
iyugov | Дата: Суббота, 26.11.2016, 23:15 | Сообщение # 471 |
iyugov
Ранг: Доцент (?)
Группа: Активисты
Должность: Инженер, учитель
|
| Сообщений: |
1191 |
| Награды: |
12 |
| Статус: |
Offline |
|
miflin,
Код (x^2 - 3x - 5) (x^4 - 6x^3 + x^2 + 24x - 14) = 0
Шесть иррациональных корней.
26.11.2016
Сообщение отредактировал iyugov - Суббота, 26.11.2016, 23:16
|
|
|
|
| |
|
|
miflin | Дата: Воскресенье, 27.11.2016, 19:36 | Сообщение # 472 |
miflin
Ранг: Профессор (?)
Хмырь обыкновенный
Группа: Пользователи
|
| Сообщений: |
2663 |
| Награды: |
87 |
| Статус: |
Offline |
|
Цитата iyugov (  ) Шесть иррациональных корней.
Оно понятно, раз шестая степень многочлена...
Я, честно, не любитель уравнений подобного типа, поэтому просто пошел сюда
и посмотрел, что к чему. 
Вопрос в другом - есть ли какой-то не очень затратный метод для решения этого уравнения?
Сколько Вам пришлось затратить времени, чтобы для начала получить вот это?
Цитата iyugov (  ) (x^2 - 3x - 5) (x^4 - 6x^3 + x^2 + 24x - 14) = 0 Добавлено (27.11.2016, 19:36)
---------------------------------------------
И ещё вопрос - как решать уравнение 4-й степени? Хотя формулы для решения есть, но это, если не ошибаюсь,
не школьный материал, в то время как уравнение, если опять же не ошибаюсь, взято из сборника
для подготовки к ЕГЭ.
27.11.2016
|
|
|
|
| |
|
|
iyugov | Дата: Воскресенье, 27.11.2016, 20:18 | Сообщение # 473 |
iyugov
Ранг: Доцент (?)
Группа: Активисты
Должность: Инженер, учитель
|
| Сообщений: |
1191 |
| Награды: |
12 |
| Статус: |
Offline |
|
Цитата miflin (  ) уравнение, если опять же не ошибаюсь, взято из сборника
Вот и я не был уверен, что все коэффициенты правильные. Перебрал все целые варианты корней, подумал над исходным разложением, ничего не нашёл. Ну, и забил уравнение в систему символьной алгебры - она и корни подсказала, и на множители (factor) разложила. Кстати, сайт по ссылке использует систему WolframAlpha. Правда, с тем решением непонятно: оно говорит о заменах, введении y и z, но по ходу решения там только x. Ну, и методически совершенно неясно, откуда брать числа, которые там предлагается прибавлять. Подозреваю, что если уравнение имеет нормальное решение, то замены переменной там есть, но какие-то другие.
27.11.2016
|
|
|
|
| |
|
|
gail-ul | Дата: Воскресенье, 27.11.2016, 20:28 | Сообщение # 474 |
gail-ul
Ранг: Первоклашка (?)
Группа: Пользователи
|
| Сообщений: |
24 |
| Награды: |
0 |
| Статус: |
Offline |
|
Это задание на классной олимпиаде в 10 классе в общеобразовательной школе
27.11.2016
|
|
|
|
| |
|
|
miflin | Дата: Воскресенье, 27.11.2016, 20:54 | Сообщение # 475 |
miflin
Ранг: Профессор (?)
Хмырь обыкновенный
Группа: Пользователи
|
| Сообщений: |
2663 |
| Награды: |
87 |
| Статус: |
Offline |
|
...
27.11.2016
Сообщение отредактировал miflin - Воскресенье, 27.11.2016, 21:07
|
|
|
|
| |
|
|
miflin | Дата: Воскресенье, 27.11.2016, 20:59 | Сообщение # 476 |
miflin
Ранг: Профессор (?)
Хмырь обыкновенный
Группа: Пользователи
|
| Сообщений: |
2663 |
| Награды: |
87 |
| Статус: |
Offline |
|
Та "решалка", куда я ходил, выдала листинг (см. прикрепление).
Это, насколько я понимаю, реализация некоего общего стандартного подхода, не учитывающего
"олимпиадность" задачи,
Цитата gail-ul (  ) Это задание на классной олимпиаде
где нужно идти не напролом, и исхитриться. 
PS Почему-то картинка здесь не воспроизводится в нормальном масштабе. 
27.11.2016
Сообщение отредактировал miflin - Воскресенье, 27.11.2016, 21:02
|
|
|
|
| |
|
|
iyugov | Дата: Воскресенье, 27.11.2016, 21:08 | Сообщение # 477 |
iyugov
Ранг: Доцент (?)
Группа: Активисты
Должность: Инженер, учитель
|
| Сообщений: |
1191 |
| Награды: |
12 |
| Статус: |
Offline |
|
miflin, исхитрение такое: берём исходное уравнение, раскладываем на множители те скобки, которые хорошо раскладываются, перегруппируем их и перемножаем обратно.
Код . (x^2 - 3x + 1)(x^2 + 3x + 2)(x^2 - 9x + 20) = -30
. (x^2 - 3x + 1)(x+1)(x+2)(x-4)(x-5) = -30
. (x^2 - 3x + 1)(x+1)(x-4)(x+2)(x-5) = -30
. (x^2 - 3x + 1)(x^2 - 3x - 4)(x^2 - 3x - 10) = -30
Теперь можно делать замену переменной, понижающую степень уравнения. Причём можно подобрать "хороший" свободный коэффициент.
Код . t = x^2 - 3x - 4
. t(t + 5)(t - 6) = -30
. t^3 - t^2 - 30t + 30 = 0
. (t - 1)(t^2 - 30) = 0
Дальше вроде понятно.
Видимо, олимпиадность задачи в том, что с самого начала надо разглядеть приведённый вид уравнения (специально разложенный на трёхчлены), нацелиться на замену переменной и искать способы заменить квадратный трёхчлен, для чего пытаться выразить всё через него. И при замене вовремя озаботиться удачным свободным коэффициентом, хотя третью степень в принципе и без этого можно решить.
27.11.2016
Сообщение отредактировал iyugov - Воскресенье, 27.11.2016, 21:21
|
|
|
|
| |
|
|
miflin | Дата: Воскресенье, 27.11.2016, 21:36 | Сообщение # 478 |
miflin
Ранг: Профессор (?)
Хмырь обыкновенный
Группа: Пользователи
|
| Сообщений: |
2663 |
| Награды: |
87 |
| Статус: |
Offline |
|
Цитата iyugov (  ) исхитрение такое
+ 
27.11.2016
|
|
|
|
| |
|
|
gail-ul | Дата: Воскресенье, 27.11.2016, 22:13 | Сообщение # 479 |
gail-ul
Ранг: Первоклашка (?)
Группа: Пользователи
|
| Сообщений: |
24 |
| Награды: |
0 |
| Статус: |
Offline |
|
а вот еще уравнение попалось, хотела исхитриться, но не получилось, либо там опечатка
х-1)(х-3)(х+2)(х+6)=72х^2
27.11.2016
|
|
|
|
| |
|
|
iyugov | Дата: Воскресенье, 27.11.2016, 23:02 | Сообщение # 480 |
iyugov
Ранг: Доцент (?)
Группа: Активисты
Должность: Инженер, учитель
|
| Сообщений: |
1191 |
| Награды: |
12 |
| Статус: |
Offline |
|
gail-ul, там по-другому можно. Сргуппировать для одинакового коэффициента при x не получается, так сделаем же одинаковыми хотя бы свободные коэффициенты.
Код . (х-1)(х-3)(х+2)(х+6)=72х^2
. (х-1)(х+6)(х+2)(х-3)=72х^2
. (х^2+5x-6)(х^2-x-6)=72х^2
. (х^2+5x-6)(х^2-x-6)-72х^2=0
Очень бы хотелось внести эти 72x^2 в левую часть в состав множителей.
Если раскрыть скобки в левой части, то получится многочлен 4-й степени.
Код . x^4 + (5-1)x^3 + (-6-6-5)x^2 + (-6)*(5-1)x + 36 - 72x^2 = 0
Мы хотим коэффициент при x^2 уменьшить на 72. Вторая степень при раскрытии скобок получается от умножения x^2 на (-6), а также от перемножения коэффициентов при x (5 и -1). Очевидно, коэффициент при x^2 должен остаться единичным, чтобы не влиять на 4-ю степень. Таким образом, нам нужно найти два коэффициента при x:
Код . (х^2+Ax-6)(х^2+Bx-6)=0
Произведение этих коэффициентов должно уменьшиться на 72, а сумма - остаться прежней, чтобы не влиять в разложении на третью и первую (вот зачем свободные коэффициенты одинаковые) степени.
Код . A+B = 5-1 = 4
. A*B = 5*(-1) - 72 = -77
. A=-7, B=11 или наоборот.
. (х^2-7x-6)(х^2+11x-6)=0
27.11.2016
Сообщение отредактировал iyugov - Понедельник, 28.11.2016, 00:06
|
|
|
|
| |
|